题目内容
18．F1，F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右焦点，过F1的直线与椭圆相交于A、B两点，则△ABF2的周长是8．分析 求得椭圆的a=2，再由椭圆的定义可得△AF2B的周长为c=4a=8．
解答 解：椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的a=2，
由椭圆的定义可得，
△AF2B的周长为c=|AB|+|AF2|+|BF2|
=（|AF2|+|AF1|）+（|BF1|+|BF2|）
=2a+2a=4a=8．
故答案为：8．
点评 本题考查椭圆的定义、方程和性质，主要考查椭圆的定义的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
8．过椭圆 $\frac{x^2}{16}$+$\frac{y^2}{9}$=1的右焦点F2作直线l交椭圆于A、B两点，F1是椭圆的左焦点，则△AF1B 的周长为（ ）
| A． | 20 | B． | 16 | C． | 12 | D． | 10 |
9．执行如图所示的程序框图，若输出i的值是11，则判断框中的横线上可以填入的最大整数为（ ）
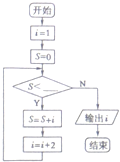
| A． | 23 | B． | 24 | C． | 25 | D． | 26 |
6．若函数y=cos（2x+$\frac{π}{3}$）的图象向左平移φ个单位后关于原点对称（|φ|＜$\frac{π}{4}$），则实数φ可以为（ ）
| A． | $-\frac{π}{6}$ | B． | $-\frac{π}{12}$ | C． | $\frac{π}{12}$ | D． | $\frac{π}{6}$ |
13．已知椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）与直线y=b相交于A、B两点，O是坐标原点，如果△AOB是等边三角形，则该椭圆的离心率为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{3}}{4}$ | D． | $\frac{\sqrt{3}}{6}$ |
已知四棱锥S-ABCD的底面为菱形，且∠ABC=60°，AB=AC=2，SA=SB=$\sqrt{2}$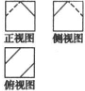
一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示，则该几何体的体积为$\frac{23}{24}$．