题目内容
设f(x)是定义在R上的偶函数,且对于任意x∈R都有f(x+1)=f(x-1).且在区间[2,3]上,f(x)=-2(x-3)2+4.(1)求
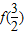 的值;
的值;(2)求出曲线y=f(x)在点
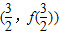 处的切线方程;
处的切线方程;(3)若矩形ABCD的两顶点A、B在x轴上,两顶点C、D在函数y=f(x)(0≤x≤2)的 图象上,求这个矩形面积的最大值.
【答案】分析:(1)根据对于任意x∈R都有f(x+1)=f(x-1)可以求得函数周期为2,再由f(x)在区间[2,4]上,f(x)=-2(x-3)2+4上的解析式,求出函数在[0,2]上的解析式,直接代入求解;
(2)求出点 ,对f(x)进行求导,根据导数与斜率的关系,求出直线的斜率,从而根据点斜式求出切线方程;
,对f(x)进行求导,根据导数与斜率的关系,求出直线的斜率,从而根据点斜式求出切线方程;
(3)已知矩形ABCD的两顶点A、B在x轴上,两顶点C、D在函数y=f(x)(0≤x≤2)的 图象上,可以求出直线在[0,2]上的解析式,设出A,B两点,根据矩形面积公式代入求出S,再利用导数求其最大值;
解答:解:(1)∵任意x∈R都有f(x+1)=f(x-1),可得f(x+2)=f(x),函数周期为2,
对设0≤x≤2,2≤x+2≤4,
可得f(x)=f(x+2)=-2(x-1)2+4,
∴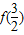 =-2(
=-2( -1)2+4=
-1)2+4= ;
;
(2)曲线y=f(x)在点( ,-
,- ),f′(x)=-4(x-3),可以k=f′(
),f′(x)=-4(x-3),可以k=f′( )=-4(
)=-4( -3)=6,
-3)=6,
∴曲线y=f(x)在点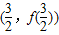 处的切线方程,
处的切线方程,
y-(- )=6(x-
)=6(x- ),化简得,y=6x-
),化简得,y=6x-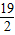 ;
;
(3)矩形ABCD的两顶点A、B在x轴上,
两顶点C、D在函数y=f(x)(0≤x≤2)的 图象上,
可以设C(x2,y2),D(x1,y1),x2>x1,A的横坐标为x1,B的横坐标为x2,
可知f(x)在区间[0,2]上,f(x)=f(x+2)=-2(x-1)2+4,
∵C(x2,y2),D(x1,y1),
∴矩形的面积为S=(x2-x1)y1=(x2-x1)[-2(x-1)2+4],
∵x1+x2=2,可得x2=2-x1,0<x1<1,
∴S=(x2-x1)[-2(x-1)2+4]=(2-x1)[-2x12-2+4x1+4]=(2x1-2)(2x12-4x1-2)=4x13-12x12+4x1+4
∴S′=12x12-24x1+4=4(3x12-6x1+1)=0,
∴x1=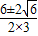 =1±
=1±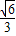 ,
,
当x>1+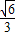 或x<1-
或x<1-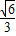 时,f′(x)>0,f(x)为增函数,
时,f′(x)>0,f(x)为增函数,
当1- <x<1+
<x<1+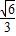 时,f′(x)<0,f(x)为增函数,
时,f′(x)<0,f(x)为增函数,
∴f(x)在x=1-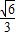 处取得极大值也是最大值,
处取得极大值也是最大值,
∴f(x)max=f(1-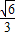 )=[2-2(1-
)=[2-2(1-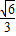 )][-2(1-
)][-2(1-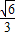 -1)2+4]=
-1)2+4]= =
=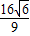 ,
,
∴这个矩形面积的最大值为: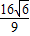 ;
;
点评:此题主要考查利用导数研究曲线上某点的切线方程以及函数周期性的利用,此题是一道中档题,计算量比较大,考查学生的计算能力.
(2)求出点
 ,对f(x)进行求导,根据导数与斜率的关系,求出直线的斜率,从而根据点斜式求出切线方程;
,对f(x)进行求导,根据导数与斜率的关系,求出直线的斜率,从而根据点斜式求出切线方程;(3)已知矩形ABCD的两顶点A、B在x轴上,两顶点C、D在函数y=f(x)(0≤x≤2)的 图象上,可以求出直线在[0,2]上的解析式,设出A,B两点,根据矩形面积公式代入求出S,再利用导数求其最大值;
解答:解:(1)∵任意x∈R都有f(x+1)=f(x-1),可得f(x+2)=f(x),函数周期为2,
对设0≤x≤2,2≤x+2≤4,
可得f(x)=f(x+2)=-2(x-1)2+4,
∴
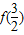 =-2(
=-2( -1)2+4=
-1)2+4= ;
;(2)曲线y=f(x)在点(
 ,-
,- ),f′(x)=-4(x-3),可以k=f′(
),f′(x)=-4(x-3),可以k=f′( )=-4(
)=-4( -3)=6,
-3)=6,∴曲线y=f(x)在点
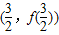 处的切线方程,
处的切线方程,y-(-
 )=6(x-
)=6(x- ),化简得,y=6x-
),化简得,y=6x-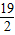 ;
;(3)矩形ABCD的两顶点A、B在x轴上,
两顶点C、D在函数y=f(x)(0≤x≤2)的 图象上,
可以设C(x2,y2),D(x1,y1),x2>x1,A的横坐标为x1,B的横坐标为x2,
可知f(x)在区间[0,2]上,f(x)=f(x+2)=-2(x-1)2+4,
∵C(x2,y2),D(x1,y1),
∴矩形的面积为S=(x2-x1)y1=(x2-x1)[-2(x-1)2+4],
∵x1+x2=2,可得x2=2-x1,0<x1<1,
∴S=(x2-x1)[-2(x-1)2+4]=(2-x1)[-2x12-2+4x1+4]=(2x1-2)(2x12-4x1-2)=4x13-12x12+4x1+4
∴S′=12x12-24x1+4=4(3x12-6x1+1)=0,
∴x1=
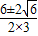 =1±
=1±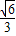 ,
,当x>1+
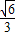 或x<1-
或x<1-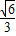 时,f′(x)>0,f(x)为增函数,
时,f′(x)>0,f(x)为增函数,当1-
 <x<1+
<x<1+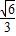 时,f′(x)<0,f(x)为增函数,
时,f′(x)<0,f(x)为增函数,∴f(x)在x=1-
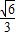 处取得极大值也是最大值,
处取得极大值也是最大值,∴f(x)max=f(1-
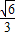 )=[2-2(1-
)=[2-2(1-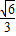 )][-2(1-
)][-2(1-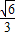 -1)2+4]=
-1)2+4]= =
=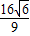 ,
,∴这个矩形面积的最大值为:
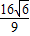 ;
;点评:此题主要考查利用导数研究曲线上某点的切线方程以及函数周期性的利用,此题是一道中档题,计算量比较大,考查学生的计算能力.

练习册系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |