题目内容
3.如图所示的程序框图,若输出的y值的取值范围是($\frac{1}{4}$,+∞),求输入的x值的取值范围.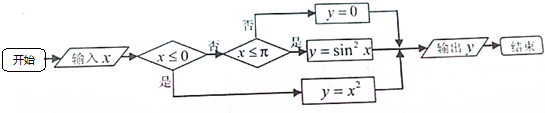
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算并输出分段函数 y=$\left\{\begin{array}{l}{\stackrel{{x}^{2}}{si{n}^{2}x}}&{\stackrel{x≤0}{0<x≤π}}\\{0}&{x>π}\end{array}\right.$的函数值.结合题中条件:“输出的y值的取值范围是($\frac{1}{4}$,+∞),”,反求出x的取值范围即可.
解答 解:模拟执行程序框图,可得程序框图的功能是计算并输出y=$\left\{\begin{array}{l}{\stackrel{{x}^{2}}{si{n}^{2}x}}&{\stackrel{x≤0}{0<x≤π}}\\{0}&{x>π}\end{array}\right.$的值.
解:当x>π时,由y=0,不符合条件,
当0<x≤π时,得sinx∈[0,1],y=sin2x∈[0,1],从而可得:当$\frac{π}{6}$<x<$\frac{5π}{6}$时,y=sin2x∈($\frac{1}{4}$,1],
当x≤0时,y=x2∈($\frac{1}{4}$,+∞),可解得:x$<-\frac{1}{2}$,
综上,输入的x值的取值范围是:(-∞,-$\frac{1}{2}$)∪($\frac{π}{6}$,$\frac{5π}{6}$)
点评 本题考查了选择结构的程序框图,根据框图的流程判断算法的功能是关键,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.在△ABC中,角A,B,C所对的边分别为a,b,c且满足(2b-$\sqrt{3}$c)cosA=$\sqrt{3}$acosC.
(Ⅰ)求角A的大小;
(Ⅱ)若b=4,三角形的面积S=6,求a的值.
(Ⅰ)求角A的大小;
(Ⅱ)若b=4,三角形的面积S=6,求a的值.
15.已知向量$\overrightarrow{b}$为单位向量,向量$\overrightarrow{a}$与向量$\overrightarrow{b}$夹角为60°,则对任意的正实数t,|t$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
12.对一个容量为m(m≥3,m∈N)的总体抽取容量为3的样本,当选取系统抽样方法抽取样本时,总体中每个个体被抽中的概率是$\frac{1}{3}$,则选取分层抽样抽取样本时总体中每个个体被抽中的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |