题目内容
【题目】已知两个定点![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率;
的斜率;
(3)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点.
是否过定点.
【答案】(1)![]() (2)
(2)![]() (3)线
(3)线![]() 过定点
过定点![]()
【解析】试题分析:(1)设点![]() 坐标为
坐标为![]() ,由
,由![]() ,得:
,得: ![]()
整理即可得轨迹方程;(2)依题意圆心到直线![]() 的距离
的距离![]() 即可解得直线
即可解得直线![]() 的斜率
的斜率![]() ;(3)由题意可知:
;(3)由题意可知: ![]() 四点共圆且在以
四点共圆且在以![]() 为直径的圆上,设
为直径的圆上,设![]() ,其方程为
,其方程为![]() ,即:
,即: ![]() ,又
,又![]() 在曲线
在曲线![]() 上,
上, ![]() ,即
,即![]() ,由
,由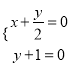 可解得定点坐标.
可解得定点坐标.
试题解析:
(1)设点![]() 坐标为
坐标为![]()
由![]() ,得:
,得: ![]()
整理得:曲线的![]() 轨迹方程为
轨迹方程为![]()
(2)依题意圆心到直线![]() 的距离
的距离![]() ,
,
![]() .
.
(3)由题意可知: ![]() 四点共圆且在以
四点共圆且在以![]() 为直径的圆上,设
为直径的圆上,设![]() ,
,
其方程为![]() ,即:
,即: ![]()
又![]() 在曲线
在曲线![]() 上,
上,
![]() ,
,
即![]() ,由
,由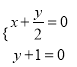 得
得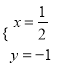 ,
,
![]() 直线
直线![]() 过定点
过定点![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目