Question

【题目】已知定义在[﹣2，2]上的函数f（x）满足f（x）+f（﹣x）=0，且 ，若f（1﹣t）+f（1﹣t2）＜0，则实数t的取值范围为 ．

Answer 1

【答案】[﹣1,1）
【解析】解：根据题意：定义在[﹣2，2]上的函数f（x）满足f（x）+f（﹣x）=0，

则函数f（x）为奇函数，

又由且 ，则函数f（x）在其定义域上为减函数，

若f（1﹣t）+f（1﹣t2）＜0，则有f（1﹣t）＜f（t2﹣1），

则有 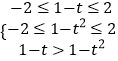，解可得﹣1≤t＜1，

即实数t的取值范围为[﹣1，1）；

所以答案是：[﹣1，1）

【考点精析】认真审题，首先需要了解奇偶性与单调性的综合(奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性)．