题目内容
9.已知函数f(x)=(sinx+cosx)2-2cos2x(x∈R).(1)求函数f(x)的周期和递增区间;
(2)若函数g(x)=f(x)-m在[0,$\frac{π}{2}$]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
分析 (1)通过二倍角公式及平方关系化简可得f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$)(x∈R),进而可得结论;
(2)∵方程g(x)=f(x)-m=0同解于方程f(x)=m在[0,$\frac{π}{2}$]上有解,通过对称性可知x1与x2关于直线x=$\frac{3π}{8}$对称,从而$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{3π}{8}$,进而可得结论.
解答 解:(1)∵f(x)=(sinx+cosx)2-2cos2x
=1+2sinxcosx-2cos2x
=sin2x-cos2x
=$\sqrt{2}$sin(2x-$\frac{π}{4}$)(x∈R),
∴函数f(x)的周期T=$\frac{2π}{2}$=π,
∵函数y=sinx的单调递增区间为:[2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$],
∴函数f(x)的周递增区间由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,
化简得:kπ-$\frac{π}{8}$≤x≤kπ+$\frac{3π}{8}$(k∈Z),即[kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$](k∈Z).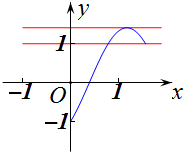
(2)∵方程g(x)=f(x)-m=0同解于f(x)=m;
在直角坐标系中画出函数f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$)在[0,$\frac{π}{2}$]上的图象,
由图象可知,当且仅当m∈[1,$\sqrt{2}$)时,
方程f(x)=m在[0,$\frac{π}{2}$]上的区间[$\frac{π}{4}$,$\frac{3π}{8}$)和($\frac{3π}{8}$,$\frac{π}{2}$]有两个不同的解x1、x2,
且x1与x2关于直线x=$\frac{3π}{8}$对称,即$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{3π}{8}$,
∴x1+x2=$\frac{3π}{4}$,
故tan(x1+x2)=tan$\frac{3π}{4}$=-1.
点评 本题考查三角函数恒等变换的应用,考查运算求解能力,注意解题方法的积累,属于中档题.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
| A. | 向左平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |