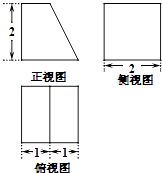
题目内容
【题目】如图,在三棱锥P﹣ABC中,AB=AC=2PA=2,∠PAB=∠PAC=∠BAC= ![]() .
.
(Ⅰ) 证明:AP⊥BC;
(Ⅱ)求三棱锥P﹣ABC的体积.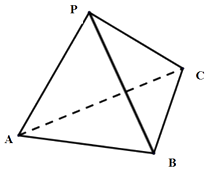
【答案】(Ⅰ)证明:由已知可得 ![]() ,
,
由余弦定理得 ![]() ,则AB2=PB2+AP2 ,
,则AB2=PB2+AP2 ,
∴AP⊥PB,同理AP⊥PC,又PB∩PC=P.
∴AP⊥平面PBC,则AP⊥BC;
(Ⅱ) 解:在Rt△APB中,由AB=2PA=2,得PB= ![]() ,
,
同理求得PC= ![]() ,又∠BAC=
,又∠BAC= ![]() ,∴BC=2,
,∴BC=2,
∴△PBC边BC上的高为 ![]() ,
,
则 ![]() .
.
∵VP﹣ABC=VA﹣PBC ,
∴ ![]()
【解析】(Ⅰ)由已知结合余弦定理求得PB、PC的长度,可得AP⊥PB,AP⊥PC,再由线面垂直的判定可得AP⊥平面PBC,则AP⊥BC;(Ⅱ)求解直角三角形可得PB=PC= ![]() ,又∠BAC=
,又∠BAC= ![]() ,得BC=2,进一步求出△PBC边BC上的高,得到
,得BC=2,进一步求出△PBC边BC上的高,得到 ![]() .结合VP﹣ABC=VA﹣PBC可得
.结合VP﹣ABC=VA﹣PBC可得
三棱锥P﹣ABC的体积.
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目