题目内容
12.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为4,左右焦点分别为F1,F2,且经过点(-3,2$\sqrt{6}$).(1)求双曲线C的方程;
(2)若P为双曲线上的一点,且|PF1||PF2|=8,求△PF1F2的周长.
分析 (1)由题意可得a2+b2=4,代入点(-3,2$\sqrt{6}$),得到a,b的方程,解方程可得a,b,进而得到双曲线的方程;
(2)运用双曲线的定义,结合条件,可得|PF1|+|PF2|=6,再由三角形的周长,计算即可得到所求.
解答 解:(1)由题意可得c=2,a2+b2=4,
代入点(-3,2$\sqrt{6}$),可得$\frac{9}{{a}^{2}}$-$\frac{24}{{b}^{2}}$=1,
解得a=1,b=$\sqrt{3}$,
即有双曲线的方程为x2-$\frac{{y}^{2}}{3}$=1;
(2)又双曲线的定义可得,||PF1|-|PF2||=2a=2,
又|PF1|•|PF2|=8,
可得(|PF1|+|PF2|)2=(|PF1|-|PF2|)2+4|PF1|•|PF2|
=4+32=36,
即有|PF1|+|PF2|=6,
则△PF1F2的周长为|PF1|+|PF2|+|F1F2|=6+4=10.
点评 本题考查双曲线的方程的求法,注意运用代入法,考查三角形的周长的求法,注意运用双曲线的定义,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.在△AOB中.已知|$\overrightarrow{OA}$|=4,|$\overrightarrow{OB}$|=3,∠AOB=60°,则$\overrightarrow{OA}$•$\overrightarrow{OB}$及△AOB的面积分别是( )
| A. | 6,6 | B. | 6,6$\sqrt{3}$ | C. | 6,3$\sqrt{3}$ | D. | 3,3$\sqrt{3}$ |
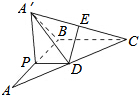 如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB边上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.
如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB边上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD. 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O,D分别是AC,PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O,D分别是AC,PC的中点,OP⊥底面ABC.