题目内容
20. 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O,D分别是AC,PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O,D分别是AC,PC的中点,OP⊥底面ABC.(1)求证:OD∥平面PAB;
(2)当k=$\frac{1}{2}$时,求直线PA与平面PBC所成角的大小.
分析 (1)根据条件便可得到OD∥PA,从而根据线面平行的判定定理即可得出OD∥平面PAB;
(2)可连接OB,容易得到OB,OC,OP三直线两两垂直,从而可分别以这三直线为x,y,z轴,建立空间直角坐标系.可设AB=1,这样根据条件即可求出图形上一些点的坐标,从而得出向量$\overrightarrow{PA},\overrightarrow{BC},\overrightarrow{BP}$的坐标,可设平面PBC的法向量为$\overrightarrow{m}=(x,y,z)$,根据$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BC}=0}\\{\overrightarrow{m}•\overrightarrow{BP}=0}\end{array}\right.$即可求出$\overrightarrow{m}$,若设直线PA与平面PBC所成角为θ,则根据sinθ=$|cos<\overrightarrow{m},\overrightarrow{BP}>|$便可求出sinθ,进而便可得到直线PA与平面PBC所成角的大小.
解答 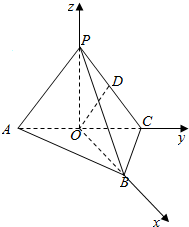 解:(1)点O,D分别是AC,PC的中点;
解:(1)点O,D分别是AC,PC的中点;
∴OD∥PA;
又PA?平面PAB;
∴OD∥平面PAB;
(2)连接OB,则OB⊥AC,又OP⊥底面ABC;
∴OB,OC,OP三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系:
设AB=1,则AC=$\sqrt{2}$,PA=2,AO=$\frac{\sqrt{2}}{2}$,$OP=\frac{\sqrt{14}}{2}$,OB=$\frac{\sqrt{2}}{2}$;
∴可得到以下几点坐标:
A($0,-\frac{\sqrt{2}}{2},0$),$P(0,0,\frac{\sqrt{14}}{2}),B(\frac{\sqrt{2}}{2},0,0),C(0,\frac{\sqrt{2}}{2},0)$;
∴$\overrightarrow{PA}=(0,-\frac{\sqrt{2}}{2},-\frac{\sqrt{14}}{2})$,$\overrightarrow{BC}=(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},0),\overrightarrow{BP}=(-\frac{\sqrt{2}}{2},0,\frac{\sqrt{14}}{2})$;
设平面PBC的法向量为$\overrightarrow{m}=(x,y,z)$,则:
$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BC}=-\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y=0}\\{\overrightarrow{m}•\overrightarrow{BP}=-\frac{\sqrt{2}}{2}x+\frac{\sqrt{14}}{2}z=0}\end{array}\right.$;
取x=1,则y=1,z=$\frac{\sqrt{7}}{7}$,∴$\overrightarrow{m}=(1,1,\frac{\sqrt{7}}{7})$;
设直线PA与平面PBC所成角为θ,则sinθ=$|cos<\overrightarrow{PA},\overrightarrow{m}>|$=$\frac{|\overrightarrow{PA}•\overrightarrow{m}|}{|\overrightarrow{PA}||\overrightarrow{m}|}=\frac{\sqrt{2}}{2•\sqrt{\frac{15}{7}}}=\frac{\sqrt{210}}{30}$;
∴直线PA与平面PBC所成角的大小为$arcsin\frac{\sqrt{210}}{30}$.
点评 考查线面平行的判定定理,三角形中位线的性质,等腰三角形的中线也是高线,通过建立空间直角坐标系,利用空间向量解决直线和平面所成角问题的方法,平面法向量的概念,以及能求空间点的坐标,向量夹角的余弦公式的坐标运算.

| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{7}{2}$ | D. | 1或$\frac{7}{2}$ |
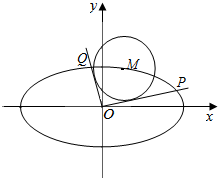 如图,已知M(x0,y0)是椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P、Q.
如图,已知M(x0,y0)是椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P、Q.