题目内容
2.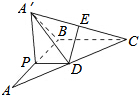 如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB边上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.
如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB边上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.(1)当棱锥A′PBCD的体积最大时,求PA的长;
(2)若点P为AB的中点,E为A′C的中点,求证:DE⊥平面A′BC.
分析 (1)令PA=x(0<x<2)求出体积表达式,利用导数确定函数的单调性,求出函数的最大值.
(2)设F为A′B的中点,连接PF,FE,通过PDEF是平行四边形,证明A′B⊥DE,又DE⊥A′C,即可得证.
解答 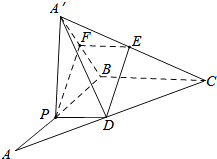 解:(1)令PA=x(0<x<2),则A′P=PD=x.BP=2-x,
解:(1)令PA=x(0<x<2),则A′P=PD=x.BP=2-x,
因为A′P⊥PD,且平面A′PD⊥平面PBCD,
故A′P⊥平面PBCD,
所以VA′-PBCD=$\frac{1}{3}$Sh=$\frac{1}{6}$(2-x)(2+x)x=$\frac{1}{6}$(4x-x3),
令f(x)=$\frac{1}{6}$(4x-x3),由f′(x)=$\frac{1}{6}$(4-3x2)=0得x=$\frac{2\sqrt{3}}{3}$,
当x∈(0,$\frac{2\sqrt{3}}{3}$)时,f′(x)>0,f(x)单调递增,
当x∈($\frac{2\sqrt{3}}{3}$,2)时,f′(x)<0,f(x)单调递减,
所以,当x=$\frac{2\sqrt{3}}{3}$时,f(x)取得最大值,
即:体积最大时,PA=$\frac{2\sqrt{3}}{3}$.
(2)设F为A′B的中点,连接PF,FE,则有EF∥BC,EF=$\frac{1}{2}$BC,PD∥BC,PD=$\frac{1}{2}$BC,
所以DE∥PF,又A′P=PB,所以PF⊥A′B.
故DE⊥A′B,
又因为点P为AB的中点,PD∥BC,可得D为AD中点,A′D=DC,又E为A′C的中点,可得:A′E=EC,
所以:DE⊥A′C,
由于A′B∩A′C=A′,可得DE⊥平面A′BC.
点评 本题主要考查了几何体的体积计算,函数最大值的求法,直线与直线的垂直的证明方法,考查了空间想象能力和计算能力,属于中档题.

| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 0 |
| A. | x-y-3=0 | B. | 2x+y-3=0 | C. | x+y-1=0 | D. | 2x-y-5=0 |
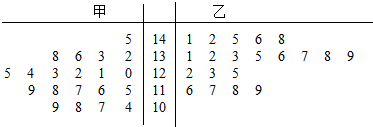
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 非优秀 | |||
| 合计 |
附表:
| P(X2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
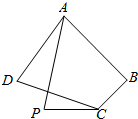 如图,在四边形ABCD中,AB=AD=4,BC=6,CD=2,3$\overrightarrow{AB}$•$\overrightarrow{AD}$+4$\overrightarrow{CB}$•$\overrightarrow{CD}$=0.
如图,在四边形ABCD中,AB=AD=4,BC=6,CD=2,3$\overrightarrow{AB}$•$\overrightarrow{AD}$+4$\overrightarrow{CB}$•$\overrightarrow{CD}$=0.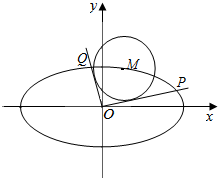 如图,已知M(x0,y0)是椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P、Q.
如图,已知M(x0,y0)是椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P、Q.