题目内容
1.已知在△ABC中,A,B的坐标分别为(-1,2),(4,3),AC的中点M在y轴上,BC的中点N在x轴上.(1)求点C的坐标;
(2)求直线MN的方程.
分析 (1)设C(x,y),根据AC的中点M在y轴上,BC的中点N在x轴上.利用中点坐标公式即可得出.
(2)由(1)利用中点坐标公式可得:yM,xN.再利用截距式即可得出直线MN的方程.
解答 解:(1)设C(x,y),∵AC的中点M在y轴上,BC的中点N在x轴上.
∴$\frac{-1+x}{2}$=0,$\frac{y+3}{2}$=0,
解得x=1,y=-3.
(2)由(1)可得:yM=$\frac{2-3}{2}$=-$\frac{1}{2}$,xN=$\frac{4+1}{2}$=$\frac{5}{2}$.
M(0,-$\frac{1}{2}$),N$(\frac{5}{2},0)$.
∴直线MN的方程是$\frac{x}{\frac{5}{2}}$+$\frac{y}{-\frac{1}{2}}$=1,化为2x-10y-5=0.
点评 本题考查了中点坐标公式、截距式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
9.已知直线l1,l2,l3的斜率分别是k1,k2,k3,其中l1∥l2,且k1,k3是方程2x2-3x-2=0的两根,则k1+k2+k3的值是( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{7}{2}$ | D. | 1或$\frac{7}{2}$ |
16.下列说法不正确的是( )
| A. | 空间中,一组对边平行且相等的四边形是一定是平行四边形 | |
| B. | 同一平面的两条垂线一定共面 | |
| C. | 三角形一定是平面图形 | |
| D. | 过一条直线有且只有一个平面与已知平面垂直 |
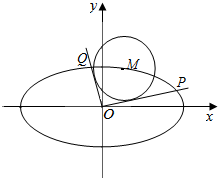 如图,已知M(x0,y0)是椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P、Q.
如图,已知M(x0,y0)是椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P、Q.