题目内容
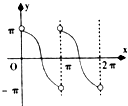
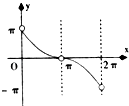
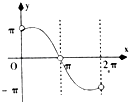
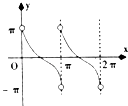
【题目】已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的图象如图所示.
)的图象如图所示.
(1)试确定该函数的解析式;
(2)该函数的图角可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
【答案】
(1)解:∵由图知:A=2,
∴T=2( ![]() ﹣
﹣ ![]() )=π,
)=π,
∴T= ![]() ,可得:ω=2,
,可得:ω=2,
∴y=2sin(2x+φ),
把( ![]() ,2)代入得2sin(
,2)代入得2sin( ![]() +φ)=2,
+φ)=2,
可得:sin( ![]() +φ)=1,
+φ)=1,
∵|φ|< ![]() ,
,
∴ ![]() +φ=
+φ= ![]() ,可得:φ=﹣
,可得:φ=﹣ ![]() ,
,
∴y=2sin(2x﹣ ![]() )
)
(2)解:y=2sin(2x﹣ ![]() )的图象可由y=sinx的图象
)的图象可由y=sinx的图象
先向右平移 ![]() 个单位长度,再保持纵坐标不变横坐标缩短为原来的
个单位长度,再保持纵坐标不变横坐标缩短为原来的 ![]() 倍,最后保持横坐标不变纵坐标伸长为原来的2倍得到.
倍,最后保持横坐标不变纵坐标伸长为原来的2倍得到.
(或先保持纵坐标不变横坐标缩短为原来的 ![]() 倍,再向右平移
倍,再向右平移 ![]() 个单位长度,最后保持横坐标不变纵坐标伸长为原来的2倍得到.)
个单位长度,最后保持横坐标不变纵坐标伸长为原来的2倍得到.)
【解析】1、根据图像可得,A=2,![]() =π,求得ω=2,把(
=π,求得ω=2,把( ![]() ,2)代入即可求得φ的值,即得函数的解析式。
,2)代入即可求得φ的值,即得函数的解析式。
2、根据函数y=Asin(ωx+φ)的图象变换可得。

练习册系列答案
相关题目