题目内容
6.在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C1:$psin(θ+\frac{π}{4})$=$\sqrt{2}$,曲线C2:$\left\{\begin{array}{l}{x=-1-2sinα}\\{y=-1+2cosα}\end{array}$,(α为参数).
(Ⅰ) 求曲线C1的直角坐标方程与曲线C2的普通方程;
(Ⅱ) 求曲线C2上的点到曲线C1的点的最小距离.
分析 (Ⅰ)由曲线C1:$psin(θ+\frac{π}{4})$=$\sqrt{2}$,展开代入$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,即可化为直角坐标方程.利用sin2α+cos2α=1可把曲线C2:$\left\{\begin{array}{l}{x=-1-2sinα}\\{y=-1+2cosα}\end{array}$,(α为参数),化为普通方程.
(II)利用点到直线的距离公式可得圆心到直线的距离,即可得出最小距离.
解答 解:(Ⅰ)由曲线C1:$psin(θ+\frac{π}{4})$=$\sqrt{2}$,展开可得:$\frac{\sqrt{2}}{2}(ρsinθ+ρcosθ)$=$\sqrt{2}$,化为直角坐标方程:x+y-2=0.
曲线C2:$\left\{\begin{array}{l}{x=-1-2sinα}\\{y=-1+2cosα}\end{array}$,(α为参数),消去参数可得(x+1)2+(y+1)2=4.
(Ⅱ) 曲线C2表示圆心为(-1,-1),半径r=2的圆,
圆心到直线的距离d$\frac{|-1-1-2|}{\sqrt{2}}$=2$\sqrt{2}$>2,
所以圆上的点到直线的距离的最小值为$2\sqrt{2}$-2..
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
18.已知双曲线x2-$\frac{{y}^{2}}{3}$=1的左、右焦点分别为F1,F2双曲线的离心率为e,若双曲线上一点P使$\frac{sin∠PF{{\;}_{2}F}_{1}}{sin∠P{F}_{1}{F}_{2}}$=e,Q点为直线PF1上的一点,且$\overrightarrow{PQ}$=3$\overrightarrow{Q{F}_{1}}$,则$\overrightarrow{{F}_{2}Q}$•$\overrightarrow{F{{\;}_{2}F}_{1}}$的值为( )
| A. | $\frac{25}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
14.某校鲁班学习小组利用课余时间模拟制作奥运圣火采集器,已知他们制作采集器的抛物面的轴切线为经过定点P(1,2)的抛物线,则该抛物线的焦点与双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1在一三象限内的渐近线的距离为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$或$\frac{1}{16}$ | C. | $\frac{1}{16}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{1}{16}$ |
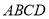 的顶点都在抛物线
的顶点都在抛物线 上,且
上,且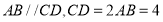 ,
, ,则点
,则点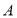 到抛物线的焦点的距离是______________.
到抛物线的焦点的距离是______________.