题目内容
不等式(m-2)x2+2(m-2)x-4≤0对一切实数x都成立,则实数m的取值范围是( )A.-2<m<2
B.-2≤m≤2
C.-2≤m<2
D.-2<m≤2
【答案】分析:等式(m-2)x2+2(m-2)x-4≤0对一切实数x都成立,包括两种情况,一是二次项及一次项系数全为0,常数项小于等于0,而是二次项系数小于0,△小于等于0,分类讨论后,综合讨论结果,即可得到答案.
解答:解:当m=2时,不等式(m-2)x2+2(m-2)x-4≤0可化为-4≤0对一切实数x都成立,
故m=2满足条件;
当m<2时,若不等式(m-2)x2+2(m-2)x-4≤0对一切实数x都成立,
则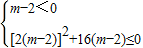
解得-2≤m<2
综上满足条件的实数m的取值范围是-2≤m≤2
故选B
点评:本题考查的知识点是二次函数的性质,其中解答时容易忽略m=2时,不等式(m-2)x2+2(m-2)x-4≤0可化为-4≤0对一切实数x都成立,而错选C
解答:解:当m=2时,不等式(m-2)x2+2(m-2)x-4≤0可化为-4≤0对一切实数x都成立,
故m=2满足条件;
当m<2时,若不等式(m-2)x2+2(m-2)x-4≤0对一切实数x都成立,
则
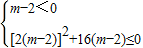
解得-2≤m<2
综上满足条件的实数m的取值范围是-2≤m≤2
故选B
点评:本题考查的知识点是二次函数的性质,其中解答时容易忽略m=2时,不等式(m-2)x2+2(m-2)x-4≤0可化为-4≤0对一切实数x都成立,而错选C

练习册系列答案
相关题目