题目内容
(2011•湖北)如图,直角坐标系xOy所在平面为α,直角坐标系x′Oy′(其中y′与y轴重合)所在的平面为β,∠xOx′=45°.
(1)已知平面β内有一点P′(2 ,2),则点P′在平面α内的射影P的坐标为 _________ ;
,2),则点P′在平面α内的射影P的坐标为 _________ ;
(2)已知平面β内的曲线C′的方程是(x′﹣ )2+2y2﹣2=0,则曲线C′在平面α内的射影C的方程是 _________ .
)2+2y2﹣2=0,则曲线C′在平面α内的射影C的方程是 _________ .

(1)已知平面β内有一点P′(2
 ,2),则点P′在平面α内的射影P的坐标为 _________ ;
,2),则点P′在平面α内的射影P的坐标为 _________ ;(2)已知平面β内的曲线C′的方程是(x′﹣
 )2+2y2﹣2=0,则曲线C′在平面α内的射影C的方程是 _________ .
)2+2y2﹣2=0,则曲线C′在平面α内的射影C的方程是 _________ .
(2,2);(x﹣1)2+y2=1.
(1)由题意知点P′在平面上的射影P距离x轴的距离不变是2,
距离y轴的距离变成2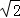 cos45°=2,
cos45°=2,
∴点P′在平面α内的射影P的坐标为(2,2)
(2)设(x′﹣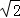 )2+2y2﹣2=0上的任意点为A(x0,y0),A在平面α上的射影是(x,y)
)2+2y2﹣2=0上的任意点为A(x0,y0),A在平面α上的射影是(x,y)
根据上一问的结果,得到x=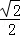 x0,y=y0,
x0,y=y0,
∵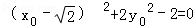 ,
,
∴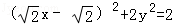
∴(x﹣1)2+y2=1,
故答案为:(2,2);(x﹣1)2+y2=1.
距离y轴的距离变成2
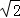 cos45°=2,
cos45°=2,∴点P′在平面α内的射影P的坐标为(2,2)
(2)设(x′﹣
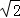 )2+2y2﹣2=0上的任意点为A(x0,y0),A在平面α上的射影是(x,y)
)2+2y2﹣2=0上的任意点为A(x0,y0),A在平面α上的射影是(x,y)根据上一问的结果,得到x=
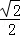 x0,y=y0,
x0,y=y0,∵
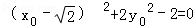 ,
,∴
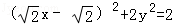
∴(x﹣1)2+y2=1,
故答案为:(2,2);(x﹣1)2+y2=1.

练习册系列答案
相关题目

 与已知圆
与已知圆 的交点,且在两坐标轴上的四个截距之和为8的圆的方程。
的交点,且在两坐标轴上的四个截距之和为8的圆的方程。 与圆心为
与圆心为 的圆
的圆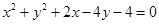 相交于
相交于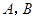 两点,且
两点,且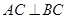 ,则实数
,则实数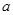 的值为_________.
的值为_________.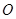 的割线
的割线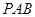 交圆
交圆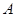 、
、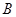 两点,割线
两点,割线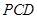 经过圆心
经过圆心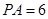 ,
,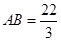 ,
,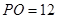 ,则圆
,则圆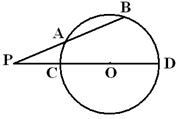
 (a>0,b>0)与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为________.
(a>0,b>0)与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为________. 是抛物线
是抛物线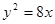 的焦点,点
的焦点,点 、
、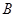 分别在抛物线
分别在抛物线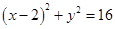
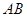 总是平行于
总是平行于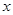 轴,,则
轴,,则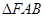 的周长的取值范围是_______________.
的周长的取值范围是_______________.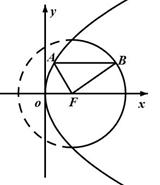
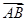 =3
=3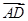 ,E、F为另一直径的两个端点,则
,E、F为另一直径的两个端点,则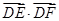 =( )
=( )