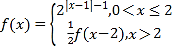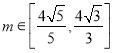题目内容
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(Ⅱ)![]()
![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(Ⅲ)若对任意的![]() 恒有
恒有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)函数![]() 的极小值为
的极小值为![]() ,无极大值;(Ⅱ)当
,无极大值;(Ⅱ)当![]() 时,函数
时,函数![]() 的在定义域
的在定义域![]() 单调递增;当
单调递增;当![]() 时,在区间
时,在区间![]() ,
,![]() 上
上![]() 单调递减,在区间
单调递减,在区间![]() 上
上![]() 单调递增;当
单调递增;当![]() 时,在区间
时,在区间![]() ,
,![]() 上
上![]() 单调递减,在区间
单调递减,在区间![]() ,上
,上![]() 单调递增.
单调递增.
(Ⅲ)![]() .
.
【解析】
试题(1)函数![]() 的定义域为
的定义域为![]() , 当
, 当![]() 时,函数
时,函数![]() ,利用导函数求出函数
,利用导函数求出函数![]() 的单调性,即可求出函数
的单调性,即可求出函数![]() 的极值;
的极值;
(2)由![]() ,所以
,所以![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,对
,对![]() 、
、![]() 、
、![]() 分类讨论,求出
分类讨论,求出![]() 的单调性;
的单调性;
(3)若对任意的![]()
![]() 恒有
恒有![]() 成立,等价于当
成立,等价于当![]() ,对任意的
,对任意的![]() ,恒有
,恒有![]() 成立,由(Ⅱ)知
成立,由(Ⅱ)知![]() ,
,![]() ,所以上式化为对任意的
,所以上式化为对任意的![]() ,恒有
,恒有![]() 成立,即
成立,即![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() .
.![]() ,令
,令![]() ,
,
得![]() ;
;![]() (舍去).
(舍去).
当![]() 变化时,
变化时,![]() 的取值情况如下:
的取值情况如下:
|
|
|
|
| — | 0 |
|
| 减 | 极小值 | 增 |
所以,函数![]() 的极小值为
的极小值为![]() ,无极大值.
,无极大值.
(2)![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 的在定义域
的在定义域![]() 单调递减;
单调递减;
当![]() 时,在区间
时,在区间![]() ,
,![]() ,上
,上![]() ,
,![]() 单调递减,
单调递减,
在区间![]() ,上
,上![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,在区间
时,在区间![]() ,
,![]() ,上
,上![]() ,
,![]() 单调递减,
单调递减,
在区间![]() ,上
,上![]() ,
,![]() 单调递增.
单调递增.
(3)由(2)知当![]() 时,函数
时,函数![]() 在区间
在区间![]() 单调递减;所以,当
单调递减;所以,当![]() 时,
时,![]() ,
,![]()
问题等价于:对任意的![]() ,恒有
,恒有![]() 成立,即
成立,即![]() ,因为a<0,
,因为a<0,![]() ,
,![]() 所以,实数
所以,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】为了普及环保知识,增强环保意识,某大学从理工类专业的![]() 班和文史类专业的
班和文史类专业的![]() 班各抽取
班各抽取![]() 名同学参加环保知识测试,统计得到成绩与专业的列联表:( )
名同学参加环保知识测试,统计得到成绩与专业的列联表:( )
优秀 | 非优秀 | 总计 | |
| 14 | 6 | 20 |
| 7 | 13 | 20 |
总计 | 21 | 19 | 40 |
附:参考公式及数据:
(1)统计量:![]() ,(
,(![]() ).
).
(2)独立性检验的临界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
则下列说法正确的是
A. 有![]() 的把握认为环保知识测试成绩与专业有关
的把握认为环保知识测试成绩与专业有关
B. 有![]() 的把握认为环保知识测试成绩与专业无关
的把握认为环保知识测试成绩与专业无关
C. 有![]() 的把握认为环保知识测试成绩与专业有关
的把握认为环保知识测试成绩与专业有关
D. 有![]() 的把握认为环保知识测试成绩与专业无关
的把握认为环保知识测试成绩与专业无关