题目内容
(本题满分12分)某单位用2 160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2 000平方米的楼房,经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
15层。
解析试题分析:设将楼房建为x层,则每平方米的平均购地费用为: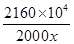 =
=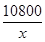 (元). 2分
(元). 2分
故每平方米的平均综合费用为:
y=560+48x+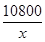 =560+48(x+
=560+48(x+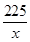 ). 6分
). 6分
当x+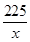 最小时,y有最小值.
最小时,y有最小值.
∵x>0,∴x+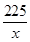 ≥2
≥2 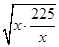 =30, 8分
=30, 8分
当且仅当x=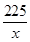 ,即x=15时上式等号成立. 10分
,即x=15时上式等号成立. 10分
所以当x=15时,y有最小值2 000元.
答:该楼房建为15层时,每平方米的平均综合费用最小. 12分
考点:函数的实际应用题;基本不等式。
点评:本题考查函数模型的建立及解决实际问题的能力,同时也考查学生的计算能力,属于基础题型。

练习册系列答案
相关题目
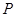 (元)之间的关系为
(元)之间的关系为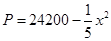 ,且生产
,且生产 吨的成本为
吨的成本为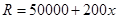 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)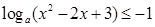 ,当
,当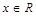 时恒成立.求
时恒成立.求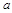 的取值范围.
的取值范围.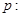 方程
方程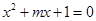 有两个不等的正实数根,命题
有两个不等的正实数根,命题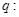 方程
方程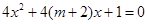 无实数根。若“
无实数根。若“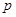 或
或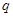 ”为真命题,求
”为真命题,求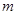 的取值范围。
的取值范围。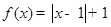
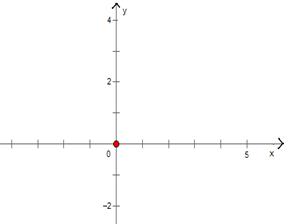
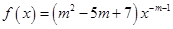
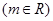 为偶函数.
为偶函数.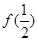 的值;
的值;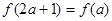 ,求实数
,求实数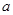 的值.
的值.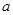 为非负实数,函数
为非负实数,函数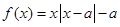 .
.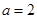 时,求函数的单调区间;
时,求函数的单调区间;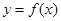 的零点个数,并求出零点.
的零点个数,并求出零点.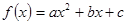 .
.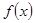 在
在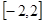 上的最大值、最小值分别是
上的最大值、最小值分别是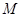 、
、 ,集合
,集合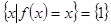 ,且
,且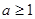 ,记
,记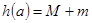 ,求
,求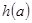 的最小值.
的最小值.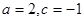 时,
时,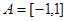 ,不等式
,不等式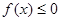 的解集为C,且
的解集为C,且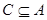 ,求实数
,求实数 的取值范围;
的取值范围;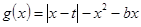
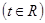 ,求
,求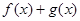 的最小值.
的最小值. 的不等式:
的不等式: