Question

【题目】已知椭圆的焦点在x轴上，一个顶点为，离心率为，过椭圆的右焦点F的直线l与坐标轴不垂直，且交椭圆于A，B两点．

求椭圆的方程；

设点C是点A关于x轴的对称点，在x轴上是否存在一个定点N，使得C，B，N三点共线？若存在，求出定点的坐标；若不存在，说明理由；

设，是线段为坐标原点上的一个动点，且，求m的取值范围．

Answer 1

【答案】（1）；（2）定点（3）

【解析】

（1）根据椭圆的一个顶点，即b＝1，利用离心率求得a和c关系进而求得a，则椭圆的方程可得；（2）设存在N（t，0），使得C、B、N三点共线，则∥，利用向量共线定理可得t，即可得出．（3）设直线l的方程为y＝k（x﹣2）（k≠0），代入椭圆方程，利用韦达定理结合向量的数量积公式，即可求得m的取值范围；

由椭圆的焦点在x轴上，设椭圆C的方程为，

椭圆C的一个顶点为，即

由，解得：，

所以椭圆C的标准方程为；

由得，设，，

设直线l的方程为，代入椭圆方程，消去y可得

则，，

点C与点A关于x轴对称，

假设存在，使得C、B、N三点共线，

则，，

、B、N三点共线，

，

，

即，

．

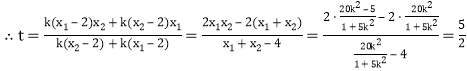存在定点，使得C、B、N三点共线．

由，

，

，

，

，

，

解得：，

当时，符合题意

故m的范围为