题目内容
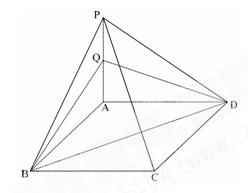
:如图,四边形ABCD是正方形,PB^平面ABCD,MA∥PB,PB=AB=2MA.
(Ⅰ)证明:AC∥平面PMD;
(Ⅱ)求直线BD与平面PCD所成的角的大小;
(Ⅲ)求平面PMD与平面ABCD所成的二面角(锐角)的正切值.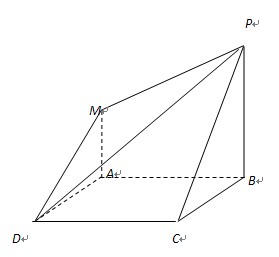
(Ⅰ)证明:AC∥平面PMD;
(Ⅱ)求直线BD与平面PCD所成的角的大小;
(Ⅲ)求平面PMD与平面ABCD所成的二面角(锐角)的正切值.

:略
:(Ⅰ)证明:如图,取PD的中点E,连EO,EM.
∵EO∥PB,EO=PB,MA∥PB,MA=PB,∴EO∥MA,且EO=MA.
∴四边形MAOE是平行四边形.∴ME∥AC.
又∵AC(/平面PMD,MEÌ平面PMD, ∴AC∥平面PMD. …………3分
(Ⅱ)如图,PB^平面ABCD,CDÌ平面ABCD,∴CD^PB.
又∵CD^BC,∴CD^平面PBC. ∵CDÌ平面PCD,∴平面PBC^平面PCD.
过B作BF^PC于F,则BF^平面PDC,连DF,则DF为BD在平面PCD上的射影.
∴ÐBDF是直线BD与平面PDC所成的角.
不妨设AB=2,则在Rt△PBC中,PB=BC=2,BF^PC,∴BF=PC=.
∵BD=2.∴在Rt△BFD中,BF=BD,∴ÐBDF=.
∴直线BD与平面PCD所成的角是. ………………5分
(Ⅲ)解:如图,分别延长PM,BA,设PM∩BA=G,连DG,
则平面PMD∩平面ABCD=DG.
不妨设AB=2,∵MA∥PB,PB=2MA,∴GA=AB=2.
过A作AN^DG于N,连MN. ∵PB^平面ABCD,
 ∴MA^平面ABCD,∴MN^DG.∴ÐMNA是平面PMD与平面ABCD
∴MA^平面ABCD,∴MN^DG.∴ÐMNA是平面PMD与平面ABCD
所成的二面角的平面角(锐角).在Rt△MAN中,
tanÐMNA==.
∴平面PMD与平面ABCD所成的二面角的正切值是
∵EO∥PB,EO=PB,MA∥PB,MA=PB,∴EO∥MA,且EO=MA.
∴四边形MAOE是平行四边形.∴ME∥AC.
又∵AC(/平面PMD,MEÌ平面PMD, ∴AC∥平面PMD. …………3分
(Ⅱ)如图,PB^平面ABCD,CDÌ平面ABCD,∴CD^PB.
又∵CD^BC,∴CD^平面PBC. ∵CDÌ平面PCD,∴平面PBC^平面PCD.
过B作BF^PC于F,则BF^平面PDC,连DF,则DF为BD在平面PCD上的射影.
∴ÐBDF是直线BD与平面PDC所成的角.
不妨设AB=2,则在Rt△PBC中,PB=BC=2,BF^PC,∴BF=PC=.
∵BD=2.∴在Rt△BFD中,BF=BD,∴ÐBDF=.
∴直线BD与平面PCD所成的角是. ………………5分
(Ⅲ)解:如图,分别延长PM,BA,设PM∩BA=G,连DG,
则平面PMD∩平面ABCD=DG.
不妨设AB=2,∵MA∥PB,PB=2MA,∴GA=AB=2.
过A作AN^DG于N,连MN. ∵PB^平面ABCD,
 ∴MA^平面ABCD,∴MN^DG.∴ÐMNA是平面PMD与平面ABCD
∴MA^平面ABCD,∴MN^DG.∴ÐMNA是平面PMD与平面ABCD所成的二面角的平面角(锐角).在Rt△MAN中,
tanÐMNA==.
∴平面PMD与平面ABCD所成的二面角的正切值是

练习册系列答案
相关题目
 中,
中, ,
,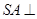 面
面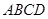 ,
, ,
,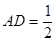 。
。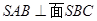 ;
;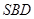 的距离。
的距离。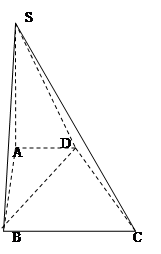
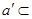 平面
平面 ,直线
,直线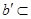 平面
平面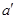 ∥
∥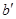 ,其中
,其中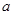 和直线
和直线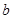 在平面
在平面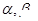 是两个相交平面, 点
是两个相交平面, 点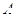 不在
不在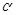 内, 也不在
内, 也不在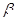 内, 则过点
内, 则过点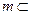 平面
平面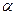 ,则“平面
,则“平面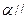 平面
平面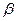 ”是“
”是“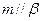 ”的
”的
 形
形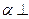 平面
平面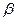 ,
,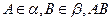 与两平面
与两平面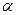 、
、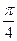 和
和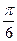 。过A、B分别作两平面交线的垂线,垂足为
。过A、B分别作两平面交线的垂线,垂足为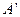 、
、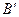 ,若AB=12,则
,若AB=12,则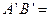 ( )
( )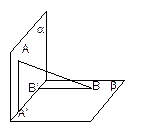
 是B1 B2 和B2 B3的中点,现沿AC,AD及CD把这个正方形折成
是B1 B2 和B2 B3的中点,现沿AC,AD及CD把这个正方形折成 一个四面体,使B1 ,B2 ,B3三点重合,重合后的点记为B,则四面体
一个四面体,使B1 ,B2 ,B3三点重合,重合后的点记为B,则四面体 对
对