题目内容
在电阻碳含量对于电阻的效应研究中,得到如下表所示的数据:
| 含碳量 (x/%) | 0.10 | 0.30 | 0.40 | 0.55 | 0.70 | 0.80 | 0.95 |
| 20 ℃时电阻 (y/Ω) | 15 | 18 | 19 | 21 | 22.6 | 23.8 | 26 |
(2)求出电阻y关于含碳量x之间的回归直线方程.
(1) r>r0.05 y与x之间有很强的线性相关关系 (2) =12.540x+13.961
=12.540x+13.961
解析解:(1) ≈0.543,
≈0.543, ≈20.771,
≈20.771,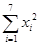 =2.595,
=2.595,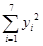 =3 104.2,
=3 104.2,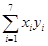 =85.61.
=85.61.
代入公式,得r=
=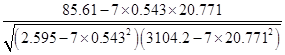
≈0.996>r0.05.
故y与x之间有很强的线性相关关系.
(2) =
=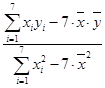 =
=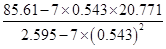
≈12.540, =
= -
-
 =20.771-12.540×0.543≈13.961,
=20.771-12.540×0.543≈13.961,
∴电阻y关于含碳量x之间的回归直线方程是 =12.540x+13.961.
=12.540x+13.961.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
为了对新产品进行合理定价,对该产品进行了试销试验,以观察需求量Y(单位:千件)对于价格x(单位:千元)的反应,得数据如下:
| x/千元 | 50 | 70 | 80 | 40 | 30 | 90 | 95 | 97 |
| y/千件 | 100 | 80 | 60 | 120 | 135 | 55 | 50 | 48 |
(2)若成本x=y+500,试求:
①在盈亏平衡条件下(利润为零)的价格;
②在利润为最大的条件下,定价为多少?
某工厂生产 、
、 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
 |  |  |  |  |  |
| B |  |  |  |  |  |
 、
、 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 、
、 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(1)求表格中
 与
与 的值;
的值;(2)从被检测的
 件
件 种元件中任取
种元件中任取 件,求
件,求 件都为正品的概率.
件都为正品的概率. 下表是对某市8所中学学生是否吸烟进行调查所得的结果:
| | 吸烟学生 | 不吸烟学生 |
| 父母中至少有一人吸烟 | 816 | 3 203 |
| 父母均不吸烟 | 188 | 1 168 |
(2)在父母均不吸烟的学生中,估计吸烟学生所占的百分比是多少?
(3)学生的吸烟习惯和父母是否吸烟有关吗?请简要说明理由.
(4)有多大的把握认为学生的吸烟习惯和父母是否吸烟有关?
某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
| 组 数 | 分 组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |

(1)补全频率分布直方图并求n,a,p的值.
(2)为调查该地区的年龄与生活习惯和是否符合低碳观念有无关系,调查组按40岁以下为青年,40岁以上(含40岁)为老年分成两组,请你先完成下面2×2列联表,并回答是否有99%的把握认为该地区的生活习惯是否符合低碳观念与人的年龄有关.
参考公式:χ2=

| P(χ2≥x0) | 0.050 | 0.010 | 0.001 |
| x0 | 3.841 | 6.635 | 10.828 |
| 年龄组 是否低碳族 | 青 年 | 老 年 | 总 计 |
| 低碳族 | | | |
| 非低碳族 | | | |
| 总计 | | | |
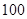 名年龄段在
名年龄段在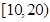 ,
,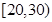 ,
, ,
,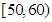 的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
的市民进行问卷调查,由此得到样本的频率分布直方图如图所示. 的人数;
的人数;  岁的人中按年龄段分层抽样的方法随机抽取
岁的人中按年龄段分层抽样的方法随机抽取 人,求
人,求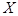 为年龄在
为年龄在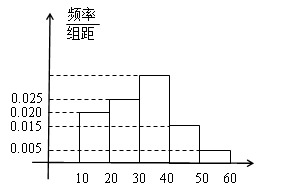

 本月价格指数
本月价格指数 上月价格指数.规定:当
上月价格指数.规定:当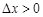 时,称本月价格指数环比增长;
时,称本月价格指数环比增长; 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当 时,称本月价格指数环比持平.
时,称本月价格指数环比持平.