题目内容
19.若不等式t2+at+1≥0对$0<t≤\frac{1}{2}$恒成立,实数a的最小值是-$\frac{5}{2}$.分析 因为函数对$0<t≤\frac{1}{2}$恒成立,分离参数a,利用均值不等式即可求出最小值.
解答 解:若不等式t2+at+1≥0对$0<t≤\frac{1}{2}$恒成立,则at≥-t2-1,所以$a≥\frac{-{t}^{2}-1}{t}=-(t+\frac{1}{t})$,∵$t+\frac{1}{t}≥2$,
当且仅当t=2时取等号.但是$0<t≤\frac{1}{2}$,
所以根据函数$y=t+\frac{1}{t}$得单调性,当t=$\frac{1}{2}$时取最小值$\frac{5}{2}$.
所以a的最小值为-$\frac{5}{2}$
故答案为:-$\frac{5}{2}$
点评 本题主要考查函数恒成立问题,利用均值不等式时取不到等号,要利用单调性来处理问题的方法,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
5.已知全集U=R,M={x|x2<2x},则∁UM=( )
| A. | {x|X≥2} | B. | {x|x>2} | C. | {x|x≤0或x≥2} | D. | {x|0<x<2} |
7.设i是虚数单位,若z=cosθ+isinθ且对应的点位于复平面的第二象限,则θ位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.某学生对一些对数进行运算,如图表格所示:
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是( )
| x | 0.21 | 0.27 | 1.5 | 2.8 |
| lgx | 2a+b+c-3(1) | 6a-3b-2(2) | 3a-b+c(3) | 1-2a+2b-c(4) |
| x | 3 | 5 | 6 | 7 |
| lgx | 2a-b(5) | a+c(6) | 1+a-b-c(7) | 2(a+c)(8) |
| x | 8 | 9 | 14 | |
| lgx | 3-3a-3c(9) | 4a-2b(10) | 1-a+2b(11) |
| A. | (3),(8) | B. | (4),(11) | C. | (1),(3) | D. | (1),(4) |
11.(2x+1)5(x2-$\frac{2}{x}$+$\frac{1}{{x}^{4}}$)的展开式的常数项是( )
| A. | 100 | B. | -100 | C. | 60 | D. | -60 |
9.已知全集U=R,A={x|x<1},B={y|-|x|+y=2},则集合∁U(A∪B)=( )
| A. | {x|1≤x<2} | B. | {x|1<x≤2} | C. | {x|x≥1} | D. | {x|x≤2} |
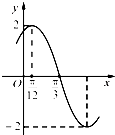 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )