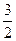题目内容
已知椭圆的中心在坐标原点,焦点在x轴上,它的一个焦点为F,M是椭圆上的任意点,|MF|的最大值和最小值的几何平均数为2,椭圆上存在着以y=x为轴的对称点M1和M2,且|M1M2|= ,试求椭圆的方程
,试求椭圆的方程
 ,试求椭圆的方程
,试求椭圆的方程椭圆方程为: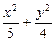 =1.
=1.
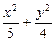 =1.
=1.|MF|max=a+c,|MF|min=a-c,则(a+c)(a-c)=a2-c2=b2,
∴b2=4,设椭圆方程为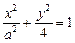 ①
①
设过M1和M2的直线方程为y=-x+m ②
将②代入①得:(4+a2)x2-2a2mx+a2m2-4a2="0 " ③
设M1(x1,y1)、M2(x2,y2),M1M2的中点为(x0,y0),
则x0=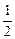 (x1+x2)=
(x1+x2)=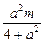 ,y0=-x0+m=
,y0=-x0+m=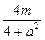 .
.
代入y=x,得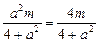 ,
,
由于a2>4,∴m=0,∴由③知x1+x2=0,x1x2=-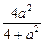 ,
,
又|M1M2|=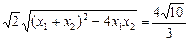 ,
,
代入x1+x2,x1x2可解a2=5,故所求椭圆方程为: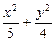 =1.
=1.
∴b2=4,设椭圆方程为
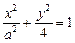 ①
①设过M1和M2的直线方程为y=-x+m ②
将②代入①得:(4+a2)x2-2a2mx+a2m2-4a2="0 " ③
设M1(x1,y1)、M2(x2,y2),M1M2的中点为(x0,y0),
则x0=
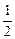 (x1+x2)=
(x1+x2)=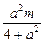 ,y0=-x0+m=
,y0=-x0+m=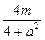 .
.代入y=x,得
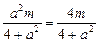 ,
,由于a2>4,∴m=0,∴由③知x1+x2=0,x1x2=-
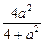 ,
,又|M1M2|=
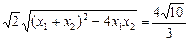 ,
,代入x1+x2,x1x2可解a2=5,故所求椭圆方程为:
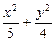 =1.
=1.
练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 +
+ =1,过点P(2,1)引一条弦,使它在这点被平分,求此弦所在的直线方程.
=1,过点P(2,1)引一条弦,使它在这点被平分,求此弦所在的直线方程.
 +y2=1(y≥0),求
+y2=1(y≥0),求 的最大值、最小值.
的最大值、最小值. ,且∠F1BF2=
,且∠F1BF2= ,求椭圆的方程.
,求椭圆的方程.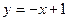 与椭圆
与椭圆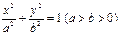 相交于A、B两点.。
相交于A、B两点.。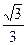 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;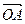 与向量
与向量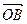 互相垂直(其中O为坐标原点),当椭圆的离心率e=2时,求椭圆的长轴的长.
互相垂直(其中O为坐标原点),当椭圆的离心率e=2时,求椭圆的长轴的长.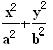 =1(a>b>0)上的两点,已知向量m(
=1(a>b>0)上的两点,已知向量m(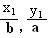 ) ,n(
) ,n(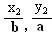 ),若m·n=0且椭圆的离心率e=
),若m·n=0且椭圆的离心率e=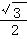 ,短轴长为2,O为坐标原点:
,短轴长为2,O为坐标原点: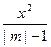 +
+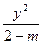 =1是焦点在y轴上的椭圆,则m的取值范围是( )
=1是焦点在y轴上的椭圆,则m的取值范围是( )