题目内容
已知向量
=(1,5),
=(-3,2),则向量
在
方向上的投影为 .
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:求出向量a,b的数量积和模,再由向量
在
方向上的投影为:
,计算即可得到.
| a |
| b |
| ||||
|
|
解答:
解:由于向量
=(1,5),
=(-3,2),
则
•
=-3+10=7,|
|=
=
,
则向量
在
方向上的投影为:
=
=
.
故答案为:
| a |
| b |
则
| a |
| b |
| b |
| 9+4 |
| 13 |
则向量
| a |
| b |
| ||||
|
|
| 7 | ||
|
7
| ||
| 13 |
故答案为:
7
| ||
| 13 |
点评:本题考查平面向量的数量积坐标表示和性质,考查向量的投影的概念,考查运算能力,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
解下列不等式:
(1)|4x-3|<21;
(2)|
+2|≥
;
(3)
>
;
(4)|x+3|>x+3;
(5)|3x-4|>2x-1;
(6)|3x-4|≤x-1.
(1)|4x-3|<21;
(2)|
| x-1 |
| 2 |
| 3 |
| 4 |
(3)
| |3x-1|-1 |
| 2 |
| |1-3x|+1 |
| 3 |
(4)|x+3|>x+3;
(5)|3x-4|>2x-1;
(6)|3x-4|≤x-1.
在四边形ABCD中,若
=
+
,则四边形ABCD的形状一定是( )
| AC |
| AB |
| AD |
| A、平行四边形 | B、菱形 |
| C、矩形 | D、正方形 |
已知数列{an}满足an+2=-an(n∈N*),且a1=1,a2=2,则该数列前2012项的和为( )
| A、-3 | B、3 | C、1 | D、0 |
设2b是1-a和1+a的等比中项,则a+4b的最大值为( )
| A、1 | ||||
| B、3 | ||||
C、
| ||||
D、
|
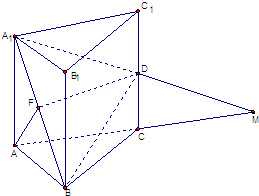 已知正三棱柱A1B1C1-ABC中,AA1=AB=a,D是CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M(如图),
已知正三棱柱A1B1C1-ABC中,AA1=AB=a,D是CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M(如图),