题目内容
【题目】已知双曲线![]() =1(a>0,b>0)的右焦点为F,P,Q为双曲线上关于原点对称的两点,若
=1(a>0,b>0)的右焦点为F,P,Q为双曲线上关于原点对称的两点,若![]() =0,且∠POF<
=0,且∠POF<![]() ,则该双曲线的离心率的取值范围为______.
,则该双曲线的离心率的取值范围为______.
【答案】![]()
【解析】
运用三角函数的定义可得|PF|=2csin∠PQF,|QF|=2ccos∠PQF,取左焦点F',连接PF',QF',可得四边形PFQF'为矩形,由双曲线的定义和矩形的性质,可得﹣2csin∠PQF+2ccos∠PQF=2a,由离心率公式,即可得到所求值.

![]() 0,可得PF⊥QF,在Rt△PQF中,|OF|=c,∴|PQ|=2c,∠POF
0,可得PF⊥QF,在Rt△PQF中,|OF|=c,∴|PQ|=2c,∠POF![]() ,0<∠PQF
,0<∠PQF![]() ,可得|PF|=2csin∠PQF,|QF|=2ccos∠PQF,取左焦点F',连接PF',QF',可得四边形PFQF'为矩形,∴||QF|﹣|PF||=|PF'|﹣|PF|=﹣2csin∠PQF+2ccos∠PQF=2a,∴e
,可得|PF|=2csin∠PQF,|QF|=2ccos∠PQF,取左焦点F',连接PF',QF',可得四边形PFQF'为矩形,∴||QF|﹣|PF||=|PF'|﹣|PF|=﹣2csin∠PQF+2ccos∠PQF=2a,∴e![]() ∈(1,
∈(1,![]() ).
).
故答案为:(1,![]() ).
).

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】已知直线![]() .
.
(1)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(2)若直线![]() 交
交![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,求
,求![]() 的面积的最小值并求此时直线
的面积的最小值并求此时直线![]() 的方程;
的方程;
(3)已知点![]() ,若点
,若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值并求此时直线
的最大值并求此时直线![]() 的方程.
的方程.
【题目】某班同学利用国庆节进行社会实践,对![]() 的人群随机抽取
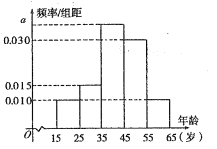
的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”.得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”.得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳组的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
(1)补全频率分布直方图,并求![]() ,
,![]() ,
,![]() 的值;
的值;

(2)求年龄段人数的中位数和众数;
(3)从![]() 岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取3人作为领队,求选取的3名领队中年龄都在
岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取3人作为领队,求选取的3名领队中年龄都在![]() 岁的概率.
岁的概率.