题目内容
(本题满分10分)已知函数 ,(
,(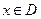 ),若同时满足以下条件:
),若同时满足以下条件:
① 在D上单调递减或单调递增
在D上单调递减或单调递增
② 存在区间[ ]
]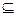 D,使
D,使 在[
在[ ]上的值域是[
]上的值域是[ ],那么称
],那么称 (
(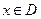 )为闭函数。
)为闭函数。
(1)求闭函数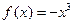 符合条件②的区间[
符合条件②的区间[ ];
];
(2)判断函数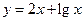 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[ ];若不是请说明理由;
];若不是请说明理由;
(3)若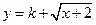 是闭函数,求实数
是闭函数,求实数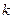 的取值范围.
的取值范围.
解:(1)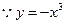 在R上单减,所以区间[
在R上单减,所以区间[ ]满足
]满足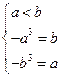
解得
(2)易知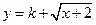 在
在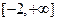 上单调递增.设满足条件B的区间为
上单调递增.设满足条件B的区间为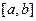 ,则方程组
,则方程组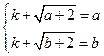 有解,即方程
有解,即方程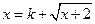 至少有两个不同的解
至少有两个不同的解
也即方程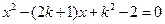 有两个都不小于
有两个都不小于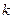 的不等根.
的不等根.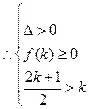 得
得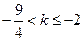 ,即位所求.
,即位所求.
另解:
(1)易知函数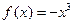 是减函数,则有
是减函数,则有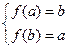 ,解得
,解得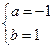 ,
,
(2)取特值说明即可,不是闭函数.
(3)由函数 是闭函数,易知函数是增函数,则在区间
是闭函数,易知函数是增函数,则在区间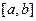 上函数的值域也是
上函数的值域也是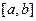 ,说明函数
,说明函数 图像与直线
图像与直线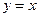 有两个不同交点,令
有两个不同交点,令
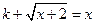 ,则有
,则有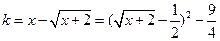 =
=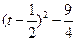 ,(令
,(令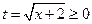 ) ,如图
) ,如图
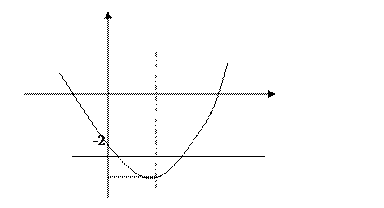
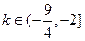
解析

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
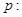 函数
函数 是增函数,
是增函数,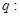 函数
函数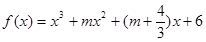 在R上有极值,求使命题“p且q”为真的实数m的取值范围。
在R上有极值,求使命题“p且q”为真的实数m的取值范围。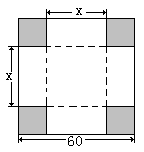
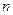 年每件小包的生产成本
年每件小包的生产成本 元,若皮制产品的销售价格不变,第
元,若皮制产品的销售价格不变,第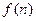 万元(今年为第一年).
万元(今年为第一年).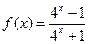 (1)解不等式
(1)解不等式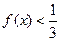 ; (2)求函数
; (2)求函数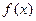 的值域.
的值域.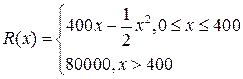 ,其中
,其中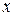 是仪器的月产量.
是仪器的月产量. ;
;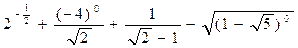
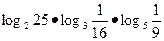 .
.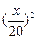 km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时
km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时 间,问运输时间最少需要多少小时?
间,问运输时间最少需要多少小时?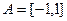 ,
,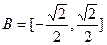 ,函数
,函数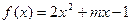 ,
,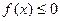 的解集为C,当
的解集为C,当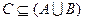 时,求实数
时,求实数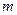 取值范围;
取值范围;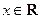 ,都有
,都有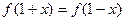 成立,试求
成立,试求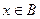 时,
时, 的值
的值 域;
域;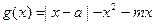
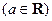 ,求
,求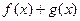 的最
的最 小值.
小值.