题目内容
在边长为60cm的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?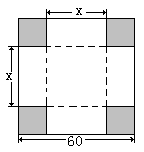
解:设箱底的边长为xcm,箱子的容积为V,则
V=x2•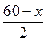 =-
=-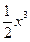 +30 x2
+30 x2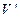 =-
=-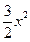 +60 x
+60 x
当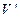 =0时,x=40或x=0(舍去),
=0时,x=40或x=0(舍去),
x=40是函数V的唯一的极值点,也就是最大值点,
当x=40时,V=1600
所以,当箱底的边长是40cm时,箱子的容积最大,最大容积是1600cm3
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
医学上为了研究传染病在传播的过程中病毒细胞的生长规律及其预防措施,将 个病毒细胞注入到一只小白鼠的体内进行试验.在试验过程中,得到病毒细胞的数量与时间的关系记录如下表:
个病毒细胞注入到一只小白鼠的体内进行试验.在试验过程中,得到病毒细胞的数量与时间的关系记录如下表:
| 时间(小时) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 病毒细胞总数(个) |  | 2 | 4 | 8 | 16 | 32 | 64 |

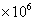 个时,小白鼠将死亡,但有一种药物对杀死此种病毒有一定效果,用药后,即可杀死其体内的大部分病毒细胞.
个时,小白鼠将死亡,但有一种药物对杀死此种病毒有一定效果,用药后,即可杀死其体内的大部分病毒细胞.(1)在16小时内,写出病毒细胞的总数
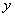 与时间
与时间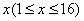 的函数关系式;
的函数关系式;(2)为了使小白鼠在实验过程中不死亡,最迟应在何时注射该种药物.(精确到整数,
 )
) 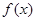 的定义域为
的定义域为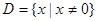 ,且满足对于任意
,且满足对于任意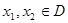 ,有
,有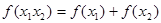 .
.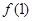 的值;
的值;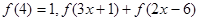 ≤
≤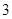 ,且
,且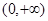 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.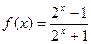 .
.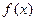 的奇偶性,并证明;
的奇偶性,并证明;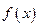 对任意的
对任意的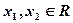 ,都有
,都有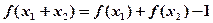 成立,且当
成立,且当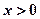 时,
时, 。
。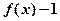 为奇函数; (2)求证:
为奇函数; (2)求证: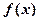 是R上的增函数;
是R上的增函数;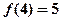 ,解不等式
,解不等式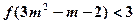 .
. ,(
,(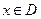 ),若同时满足以下条件:
),若同时满足以下条件: ]
]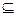 D,使
D,使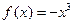 符合条件②的区间[
符合条件②的区间[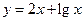 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[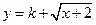 是闭函数,求实数
是闭函数,求实数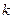 的取值范围.
的取值范围.
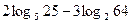
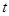 (天)的函数,且销售量近似满足函数
(天)的函数,且销售量近似满足函数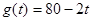 (件),价格近似满足函数
(件),价格近似满足函数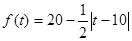 (元)。
(元)。 函数表达式;
函数表达式;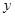 的最大值与最小值。
的最大值与最小值。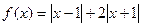
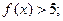
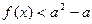 的解集为空集,求
的解集为空集,求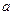 的取值范围.
的取值范围.