题目内容
 (2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=
(2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=| 2 |
(1)求平面ABB'A'与底面ABC所成的角的正切值;
(2)求侧面BB'C'C的面积.
分析:(1)求平面ABB'A'与底面ABC所成的角的正切值,首先要做出二面角的平面角,再根据它所在的三角形的特征求出角的正切,本题中侧面A1ACC1⊥面ABC,过A1向底面ABC作垂线于垂足H,则H在AC上,再在面ABC内,过H向AB作垂线于垂足D,连接A1D,则∠A1DH是面A1ABB1与底ABC所成二面角的平面角,解三角形求出此角的正切值即可得到答案;
(2)由于平行四边形的面积是一边乘以这边上的高或者相邻两边与它们夹角的正弦的乘积,考查本题的图形及题设条件,由四边形的边长易知,且两邻边夹角的正弦值易知,故可用相邻两边与它们夹角的正弦的乘积求侧面BB'C'C的面积
(2)由于平行四边形的面积是一边乘以这边上的高或者相邻两边与它们夹角的正弦的乘积,考查本题的图形及题设条件,由四边形的边长易知,且两邻边夹角的正弦值易知,故可用相邻两边与它们夹角的正弦的乘积求侧面BB'C'C的面积
解答: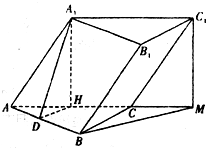 解:(1)∵侧面A1ACC1⊥面ABC.
解:(1)∵侧面A1ACC1⊥面ABC.
过A1向底面ABC作垂线于垂足H,则H在AC上
又AA1和底面ABC所成角为60°∴∠A1AC=60°,又AA1=2a
故A1H=
a,AH=a
再在面ABC内,过H向AB作垂线于垂足D,连接A1D
则∠A1DH是面A1ABB1与底ABC所成二面角的平面角
在△ABC中,∠ABC=90°,AB=BC=
a
则∠CAB=45°,AC=2a,从而DH=
a
在△A1HD中,tan∠A1DH=
=
…(6分)
(2)过C1向AC的延长线作垂线于垂足M,则C1M⊥面ABC在△BCM中,BC=
aCM=a,∠BCM=135°
∴BM2=(
a)2+a2-2•
a•a•cos135°=5a2
在Rt△BC1M中,,BC12=BM2+C1M2=8a2
在平行四边形BCC1B1中,cos∠BCC1=
=-
即sin∠BCC1=
从而□BCC1B1的面积S=BC•CC1•sin∠BCC1=
a2.…(12分)
 解:(1)∵侧面A1ACC1⊥面ABC.
解:(1)∵侧面A1ACC1⊥面ABC.过A1向底面ABC作垂线于垂足H,则H在AC上
又AA1和底面ABC所成角为60°∴∠A1AC=60°,又AA1=2a
故A1H=
| 3 |
再在面ABC内,过H向AB作垂线于垂足D,连接A1D
则∠A1DH是面A1ABB1与底ABC所成二面角的平面角
在△ABC中,∠ABC=90°,AB=BC=
| 2 |
则∠CAB=45°,AC=2a,从而DH=
| ||
| 2 |
在△A1HD中,tan∠A1DH=
| ||||
|
| 6 |
(2)过C1向AC的延长线作垂线于垂足M,则C1M⊥面ABC在△BCM中,BC=
| 2 |
∴BM2=(
| 2 |
| 2 |
在Rt△BC1M中,,BC12=BM2+C1M2=8a2
在平行四边形BCC1B1中,cos∠BCC1=
BC2+C
| ||||
| 2BC•CC1 |
| ||
| 4 |
即sin∠BCC1=
| ||
| 4 |
从而□BCC1B1的面积S=BC•CC1•sin∠BCC1=
| 7 |
点评:本题是一个与二面角有关的立体几何综合题,解题的关键是了解几何体的几何特征,根据其几何特征选择求二面角求面积的方法,本题第一小题要注意二面角平面角的做法,分为三步,作、证、求,做题时要注意不要忘记第二步的证明,第二小题求面积时根据题设条件选择相应的求面积公式很重要,本题中由于四边形的角易求,故选择了两边一夹角正弦的乘积这一方法,本题难度较大,做题时要细心谨慎

练习册系列答案
相关题目