题目内容
(2008•武汉模拟)如果关于x的方程ax+
=3有且仅有一个正实数解,那么实数a的取值范围为( )
| 1 |
| x2 |
分析:我们可将关于x的方程 ax+
=3有且仅有一个正实数解,转化为方程
=3-ax有且仅有一个正实数解,分别画出左右两式出函数的图象,结合图象法即可得到答案.
| 1 |
| x2 |
| 1 |
| x2 |
解答: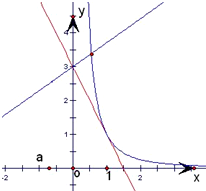 解:由关于x的方程 ax+
解:由关于x的方程 ax+
=3有且仅有一个正实数解,
转化为方程
=3-ax有且仅有一个正实数解,
分别画出左右两式出函数y=
和y=3-ax的图象,
则它们的图象有且仅有一个交点.
观察图象得:
实数a的取值范围为a≤0或a=2
故选B.
 解:由关于x的方程 ax+
解:由关于x的方程 ax+| 1 |
| x2 |
转化为方程
| 1 |
| x2 |
分别画出左右两式出函数y=
| 1 |
| x2 |
则它们的图象有且仅有一个交点.
观察图象得:
实数a的取值范围为a≤0或a=2
故选B.
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据函数的定义域,将分式方程根的个数问题转化为函数图象的个数问题是解答本题的关键.

练习册系列答案
相关题目