题目内容
7.已知R上的奇函数f(x),f(x+2)=f(x),x∈[0,1]时,f(x)=1-|2x-1|.定义:f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn-1(x)),n≥2,n∈N*,则f3(x)=$\frac{9}{8(x-1)}$在[-1,3]内所有不等实根的和为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
分析 f3(x)=$\frac{9}{8(x-1)}$在[-1,3]内的根,可化为函数f3(x)与函数y=$\frac{9}{8(x-1)}$图象交点的横坐标,作图求解即可.
解答 解:∵定义在R上的奇函数f(x),f(x+2)=f(x),
x∈[0,1]时f(x)=1-|2x-1|.
∴函数f1(x)的图象如下图所示:
∵f2(x)=f(f1(x)),
∴函数f2(x)的图象如下图所示: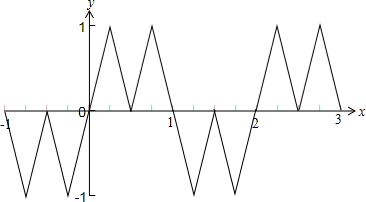
∵f3(x)=f(f2(x)),
∴作函数f3(x)与函数y=$\frac{9}{8(x-1)}$图象如下图所示: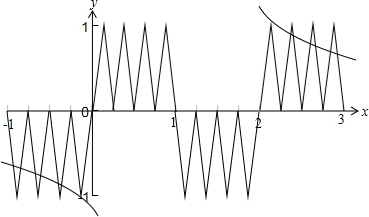
由图可知两函数图象共有14个交点,且两两关于(1,0)点对称,
故f3(x)=$\frac{9}{8(x-1)}$在[-1,3]内所有不等实根的和为14,
故选:C
点评 本题考查的知识点是函数的零点个数与方程根的关系,本题图象比较难画,属于难题.

练习册系列答案
相关题目
17.已知数列{an}的前n项和为Sn,a1=$\frac{4}{3}$,且满足3Sn+Sn-1=4(n≥2,n∈N*),若a≤-Sn+$\frac{1}{{S}_{n}}$≤b(n∈N*)恒成立,则b-a的最小值为( )
| A. | $\frac{59}{72}$ | B. | $\frac{7}{12}$ | C. | $\frac{17}{72}$ | D. | 1 |
18.全集U=R,A={x|x2>4},B={x|x<0},则A∩B=( )
| A. | {x|x<-2} | B. | {x|2<x<3} | C. | {x|x>3} | D. | {x|x<-2或2<x<3} |
15.若sinα=$\frac{1}{5}$,且α是第二象限角,则$\frac{sin2α+si{n}^{2}α}{co{s}^{2}α}$ 的值为( )
| A. | $\frac{\sqrt{6}}{4}$ | B. | -$\frac{\sqrt{6}}{4}$ | C. | $\frac{\sqrt{6}}{6}$+$\frac{1}{24}$ | D. | -$\frac{\sqrt{6}}{6}+\frac{′1}{24}$ |
2.若函数f(x)=kx+xcosx在区间(0,$\frac{π}{2}$)上单调递增,则k的最小值是( )
| A. | 1 | B. | -1 | C. | -$\frac{π}{2}$ | D. | $\frac{π}{2}$ |
19.已知$sinα=\frac{{\sqrt{5}}}{5}$,且$α∈(\frac{π}{2},π)$,则tan2α=( )
| A. | 2 | B. | $\frac{4}{3}$ | C. | -2 | D. | $-\frac{4}{3}$ |
16.y=x-ex的极大值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | 不存在 |