题目内容
【题目】已知正项数列{an}的前n项和为Sn ， 点（an ， Sn）（n∈N*）都在函数f（x）= 
的图象上．
（1）求数列{an}的通项公式；
（2）若bn=an3n ， 求数列{bn}的前n项和Tn ．
【答案】
（1）解：由题可得 
当n≥2时， 
所以 
所以 
所以（an+an﹣1）（an﹣an﹣1﹣2）=0
因为an＞0
所以an﹣an﹣1=2
当n=1时， 
，所以 
因为a1＞0，所以a1=5
所以数列{an}是以5为首项，2为公差的等差数列．
所以an=5+2（n﹣1）=2n+3
（2）解：由（1）可得 
所以 
= 
=6﹣（2n+2）3n+1
所以 
【解析】（1）利用点与函数的关系，推出递推关系式，然后求解通项公式．（2）化简数列的通项公式，利用错位相减法求和即可．
【考点精析】掌握数列的前n项和是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系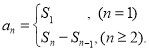
．
练习册系列答案
科学实验活动册系列答案
相关题目
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x（0＜x≤10）与销售价格y（单位：万元/辆）进行整理，得到如下的对应数据：
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
参考公式：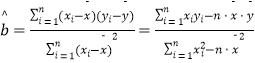 
， 
．
（1）若这两个变量呈线性相关关系，试求y关于x的回归直线方程 
；
（2）已知小王只收购使用年限不超过10年的二手车，且每辆该型号汽车的收购价格为ω=0.03x2﹣1.81x+16.2万元，根据（1）中所求的回归方程，预测x为何值时，小王销售一辆该型号汽车所获得的利润L（x）最大？ （销售一辆该型号汽车的利润=销售价格﹣收购价格）
