题目内容
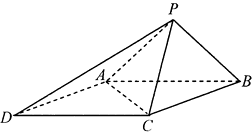
【题目】某化工厂拟建一个下部为圆柱，上部为半球的容器（如图，圆柱高为h，半径为r，不计厚度，单位：米），按计划容积为72π立方米，且h≥2r，假设其建造费用仅与表面积有关（圆柱底部不计），已知圆柱部分每平方米的费用为2千元，半球部分每平方米4千元，设该容器的建造费用为y千元． （Ⅰ）求y关于r的函数关系，并求其定义域；
（Ⅱ）求建造费用最小时的r．
【答案】解：（Ⅰ）由容积为72π立方米，得 
． 
，解得0＜r≤3，
又圆柱的侧面积为 
，
半球的表面积为2πr2 ，
所以建造费用 
，定义域为（0，3]．
（Ⅱ）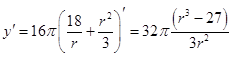 
，
又0＜r≤3，所以y'≤0，所以建造费用 ，
在定义域（0，3]上单调递减，所以当r=3时建造费用最小．
【解析】（Ⅰ）利用容积为72π立方米，列出 
，得到 
，然后求解建造费用的函数解析式．（Ⅱ）利用导函数，判断单调性求解最值即可．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
