题目内容
【题目】为发展业务,某调研组对![]() ,
,![]() 两个公司的产品需求量进行调研,准备从国内
两个公司的产品需求量进行调研,准备从国内![]() 个人口超过
个人口超过![]() 万的超大城市和
万的超大城市和![]() (
(![]() )个人口低于
)个人口低于![]() 万的小城市随机抽取若干个进行统计,若一次抽取
万的小城市随机抽取若干个进行统计,若一次抽取![]() 个城市,全是小城市的概率为
个城市,全是小城市的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)若一次抽取![]() 个城市,则:①假设取出小城市的个数为
个城市,则:①假设取出小城市的个数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
②若取出的![]() 个城市是同一类城市,求全为超大城市的概率.
个城市是同一类城市,求全为超大城市的概率.
【答案】(1)8;(2)①分布列见解析,![]() ;②
;②![]() .
.
【解析】
(1)先由题意,得到共![]() 个城市,取出2个的方法总数是
个城市,取出2个的方法总数是![]() ,其中全是小城市的情况有
,其中全是小城市的情况有![]() ,由题中数据,得到
,由题中数据,得到![]() ,求解,即可得出结果;
,求解,即可得出结果;
(2)①先由题意,得到![]() 的可能取值为
的可能取值为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求出对应的概率,进而可求出分布列,得出数学期望;
,求出对应的概率,进而可求出分布列,得出数学期望;
②分别求出四个城市全是超大城市,以及四个城市全是小城市的情况,进而可求出对应的概率.
(1)由题意,共![]() 个城市,取出2个的方法总数是
个城市,取出2个的方法总数是![]() ,其中全是小城市的情况有
,其中全是小城市的情况有![]() 种,
种,
故全是小城市的概率是![]() ,整理得
,整理得![]() ,
,
即![]() ,
,![]() ,解得
,解得![]() ;
;
(2)①由题意可知![]() 的可能取值为
的可能取值为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
故![]() 的分布列为
的分布列为
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
![]() .
.
②若4个城市全是超大城市,共![]() 有种情况;
有种情况;
若4个城市全是小城市,共有![]() 种情况;
种情况;
故全为超大城市的概率为![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】为了调查生活规律与患胃病是否与有关,某同学在当地随机调查了200名30岁以上的人,并根据调查结果制成了不完整的列联表如下:
不患胃病 | 患胃病 | 总计 | |
生活有规律 | 60 | 40 | |
生活无规律 | 60 | 100 | |
总计 | 100 |
(1)补全列联表中的数据;
(2)用独性检验的基本原理,说明生活无规律与患胃病有关时,出错的概率不会超过多少?
参考公式和数表如下:
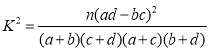
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】随着科技的发展,网购已经逐渐融入了人们的生活,在家里不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,所以选择网购的人数在逐年增加.某网店统计了2014年一2018年五年来在该网店的购买人数![]() (单位:人)各年份的数据如下表:
(单位:人)各年份的数据如下表:
年份( | 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与时间
与时间![]() (单位:年)的关系,请通过计算相关系数
(单位:年)的关系,请通过计算相关系数![]() 加以说明,(若
加以说明,(若![]() ,则该线性相关程度很高,可用线性回归模型拟合)
,则该线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式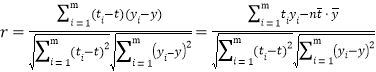
参考数据![]()
![]()
![]()
![]()
(2)该网店为了更好的设计2019年的“双十一”网购活动安排,统计了2018年“双十一”期间8个不同地区的网购顾客用于网购的时间x(单位:小时)作为样本,得到下表
地区 |
|
|
|
|
|
|
|
|
时间 | 0.9 | 1.6 | 1.4 | 2.5 | 2.6 | 2.4 | 3.1 | 1.5 |
①求该样本数据的平均数![]() ;
;
②通过大量数据统计发现,该活动期间网购时间![]() 近似服从正态分布
近似服从正态分布![]() ,如果预计2019年“双十一”期间的网购人数大约为50000人,估计网购时间
,如果预计2019年“双十一”期间的网购人数大约为50000人,估计网购时间![]() 的人数.
的人数.
(附:若随机变量![]() 服从正态分布
服从正态分布![]() 则
则![]() ,
,![]()