题目内容
【题目】已知定义域为
的函数
是奇函数.
（1）求
，判断函数
的单调性并证明.
（2）对任意的
，不等式
恒成立，求
的取值范围.
【答案】（1）
, 函数
为单调递减函数,证明见详解；
（2）
【解析】
（1）由函数是奇函数，可得
，代入可得
的值，判断函数为单调递减函数，用定义法可得证明；
（2）由函数的单调性与奇偶性，对任意的
不等式
恒成立可化为
恒成立，分离参数可得
，设
求出
的最小值，可得
的取值范围.
解：由函数是奇函数，且函数的定义域为
,故，
即
，，故
，
判断函数为单调递减函数，证明如下：
设
，
易得：
，
，故
，
故数为单调递减函数；
（2）由题意,对于任意的不等式恒成立,
可得
恒成立，由（1）可得单调递减，
故可得：对于任意的，恒成立，
故可得：
，可得
，，
设，易得为单调递减的函数，
可得
故可得
，
故的取值范围为.
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在
内，发布成绩使用等级制，各等级划分标准见下表．
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定：A，B，C三级为合格等级，D为不合格等级为了解该校高三年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计．
按照
，
，
，
，
的分组作出频率分布直方图如图1所示，样本中分数在80分及以上的所有数据的茎叶图如图2所示
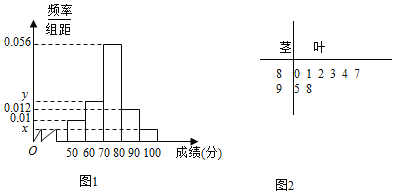
求n和频率分布直方图中的x，y的值，并估计该校高一年级学生成绩是合格等级的概率；
根据频率分布直方图，求成绩的中位数
精确到
；
在选取的样本中，从A，D两个等级的学生中随机抽取2名学生进行调研，求至少有一名学生是A等级的概率．
【题目】省环保厅对
、
、
三个城市同时进行了多天的空气质量监测，测得三个城市空气质量为优或良的数据共有180个，三城市各自空气质量为优或良的数据个数如下表所示：
|
|
| |
优（个） | 28 |
|
|
良（个） | 32 | 30 |
|
已知在这180个数据中随机抽取一个，恰好抽到记录
城市空气质量为优的数据的概率为0.2.
（1）现按城市用分层抽样的方法，从上述180个数据中抽取30个进行后续分析，求在
城中应抽取的数据的个数；
（2）已知
， 
，求在
城中空气质量为优的天数大于空气质量为良的天数的概率.