题目内容
7.在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是90°,若D1E⊥EC,则AE=1.分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设E(1,t,0),0≤t≤2,分别求出$\overrightarrow{{D}_{1}E}$和$\overrightarrow{{A}_{1}D}$,由$\overrightarrow{{D}_{1}E}$•$\overrightarrow{{A}_{1}D}$=0,能求出直线D1E与A1D所成角的大小;分别求出$\overrightarrow{{D}_{1}E}$,$\overrightarrow{EC}$,由$\overrightarrow{{D}_{1}E}•\overrightarrow{EC}$=0,能求出AE的长.
解答 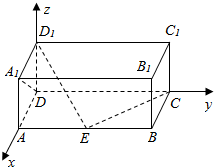 解:∵在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,
解:∵在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,
∴以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则D(0,0,0),D1(0,0,1),A(1,0,0),A1(1,0,1),C(0,2,0),
设E(1,t,0),0≤t≤2,
则$\overrightarrow{{D}_{1}E}$=(1,t,-1),$\overrightarrow{{A}_{1}D}$=(-1,0,-1),
∴$\overrightarrow{{D}_{1}E}$•$\overrightarrow{{A}_{1}D}$=-1+0+1=0,
∴直线D1E与A1D所成角的大小是90°.
∵$\overrightarrow{{D}_{1}E}$=(1,t,-1),$\overrightarrow{EC}$=(-1,2-t,0),D1E⊥EC,
∴$\overrightarrow{{D}_{1}E}•\overrightarrow{EC}$=-1+t(2-t)+0=0,
解得t=1,∴AE=1.
故答案为:900,1.
点评 本题考查异面直线所成角的大小的求法,考查线段长的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分且必要条件 | D. | 不充分也不必要条件 |
| A. | 内含 | B. | 相交 | C. | 相切 | D. | 相离 |
| A. | f(x)是奇函数 | B. | f(x)是增函数 | ||
| C. | 当x>2015时,f(x)>$\frac{1}{2}$恒成立 | D. | f(x)的最小值是-$\frac{1}{2}$. |