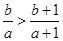题目内容
在R上定义运算：xy＝x(1－y)．若对任意x>2，不等式(x－a)x≤a＋2都成立，则实数a的取值范围是( )
| A．[－1，7] | B．(－∞，3] |
| C．(－∞，7] | D．(－∞，－1]∪[7，＋∞) |
C
由题意得(x－a)x＝(x－a)(1－x)，
故不等式(x－a)x≤a＋2化为(x－a)(1－x)≤a＋2，
化简得x2－(a＋1)x＋2a＋2≥0，
故原题等价于x2－(a＋1)x＋2a＋2≥0在(2，＋∞)上恒成立．
由二次函数f(x)＝x2－(a＋1)x＋2a＋2的图像，可知其对称轴为x＝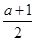
.
讨论得
或
解得a≤3或3<a≤7，综上可得a≤7.
故不等式(x－a)x≤a＋2化为(x－a)(1－x)≤a＋2，
化简得x2－(a＋1)x＋2a＋2≥0，
故原题等价于x2－(a＋1)x＋2a＋2≥0在(2，＋∞)上恒成立．
由二次函数f(x)＝x2－(a＋1)x＋2a＋2的图像，可知其对称轴为x＝
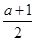.讨论得
或解得a≤3或3<a≤7，综上可得a≤7.
练习册系列答案
相关题目
<
,
,
,
中最大的是( )
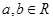，且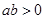
，则下列不等式中，恒成立的是
的不等式
和
的解集分别为
，
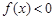和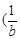
，
，那么称这两个不等式为“对偶不等式”.如果不等式
与不等式
为“对偶不等式”，且
，
，那么
= .
，则下列不等关系正确的是（ ）
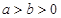，则下列不等式中总成立的是（ ）
