题目内容
【题目】已知半径为1的球O内切于正四面体A﹣BCD,线段MN是球O的一条动直径(M,N是直径的两端点),点P是正四面体A﹣BCD的表面上的一个动点,则 ![]() 的取值范围是 .
的取值范围是 .
【答案】[0,8]
【解析】解:由题意M,N是直径的两端点,可得 ![]() =
= ![]() ,
, ![]() =﹣1, 则
=﹣1, 则 ![]() =(
=( ![]() +
+ ![]() )(
)( ![]() +
+ ![]() )=
)= ![]() 2+
2+ ![]() (
( ![]() )+
)+ ![]()
= ![]() 2+0﹣1=
2+0﹣1= ![]() 2﹣1,
2﹣1,
即求正四面体表面上的动点P到O的距离的范围.
当P位于E(切点)时,OP取得最小值1;
当P位于A处时,OP即为正四面体外接球半径最大即为3.
设正四面体的边长为a,由O为正四面体的中心,
可得直角三角形ABE中,AE= ![]() a,BE=
a,BE= ![]() a,OE=
a,OE= ![]() a,AO=
a,AO= ![]() a,
a,
综上可得 ![]() 2﹣1的最小值为1﹣1=0,最大值为9﹣1=8.
2﹣1的最小值为1﹣1=0,最大值为9﹣1=8.
则 ![]() 的取值范围是[0,8].
的取值范围是[0,8].
所以答案是:[0,8].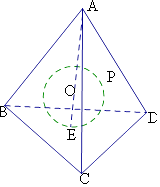

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
