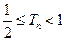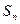题目内容
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n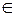
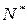 ),其中
),其中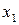 为正实数.
为正实数.
(Ⅰ)用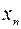 表示xn+1;
表示xn+1;
(Ⅱ)若a1=4,记an=lg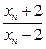 ,证明数列{
,证明数列{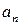 }成等比数列,并求数列{xn}的通项公式;
}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
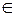
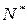 ),其中
),其中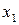 为正实数.
为正实数. (Ⅰ)用
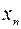 表示xn+1;
表示xn+1;(Ⅱ)若a1=4,记an=lg
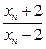 ,证明数列{
,证明数列{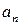 }成等比数列,并求数列{xn}的通项公式;
}成等比数列,并求数列{xn}的通项公式;(Ⅲ)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
(1)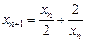 (2)见解析(3)见解析
(2)见解析(3)见解析
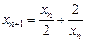 (2)见解析(3)见解析
(2)见解析(3)见解析(Ⅰ)由题可得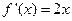 .
.
所以曲线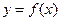 在点
在点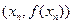 处的切线方程是:
处的切线方程是: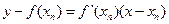 .
.
即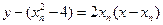 .令
.令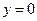 ,得
,得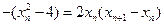 .
.
即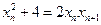 .显然
.显然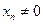 ,∴
,∴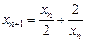 .
.
(Ⅱ)由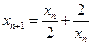 ,知
,知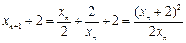 ,同理
,同理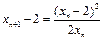 .
.
故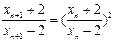 .从而
.从而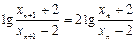 ,即
,即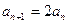 .
.
所以,数列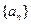 成等比数列.
成等比数列.
故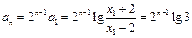 .即
.即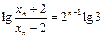 .从而
.从而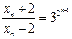 所以
所以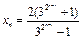
(Ⅲ)证明:由(Ⅱ)知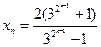 ,∴
,∴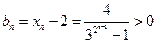
∴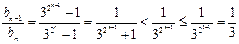 当
当 时,显然
时,显然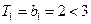 .
.
当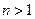 时,
时,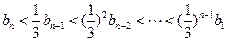
∴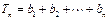
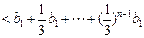
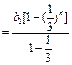
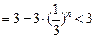 .
.
综上,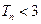
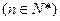 .
.
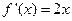 .
.所以曲线
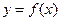 在点
在点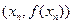 处的切线方程是:
处的切线方程是: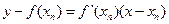 .
.即
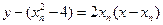 .令
.令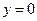 ,得
,得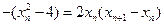 .
.即
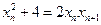 .显然
.显然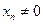 ,∴
,∴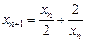 .
.(Ⅱ)由
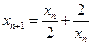 ,知
,知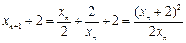 ,同理
,同理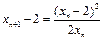 .
.故
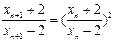 .从而
.从而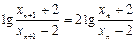 ,即
,即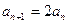 .
.所以,数列
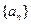 成等比数列.
成等比数列.故
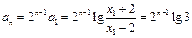 .即
.即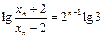 .从而
.从而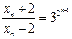 所以
所以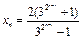
(Ⅲ)证明:由(Ⅱ)知
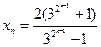 ,∴
,∴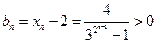
∴
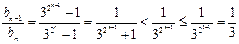 当
当 时,显然
时,显然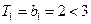 .
.当
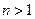 时,
时,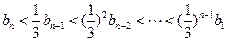
∴
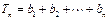
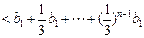
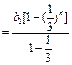
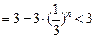 .
.综上,
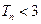
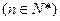 .
.
练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
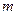 个不全相等的正数
个不全相等的正数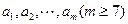 依次围成一个圆圈。
依次围成一个圆圈。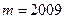 ,且
,且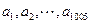 是公差为
是公差为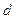 的等差数列,而
的等差数列,而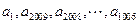 是公比为
是公比为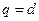 的等比数列;数列
的等比数列;数列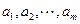 的前
的前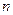 项和
项和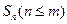 满足:
满足: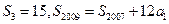 ,求通项
,求通项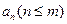 ;
;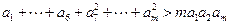 。
。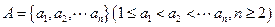 具有性质
具有性质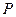 ;对任意的
;对任意的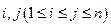 ,
,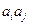 与
与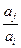 两数中至少有一个属于
两数中至少有一个属于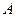 。
。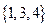 与
与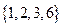 是否具有性质
是否具有性质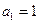 ,且
,且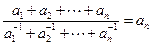 ;
;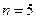 时,
时,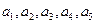 成等比数列。
成等比数列。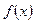 =
=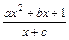 (a>0)为奇函数,且
(a>0)为奇函数,且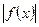 min=
min=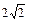 ,数列{an}与{bn}满足 如下关系:a1=2,
,数列{an}与{bn}满足 如下关系:a1=2, 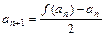 ,
,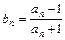 .
.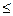
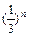 .
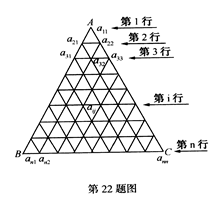
.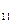 ,…第i行中第j个数为a
,…第i行中第j个数为a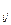 (1≤j≤i).若a
(1≤j≤i).若a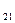 =
=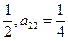
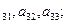
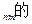 表达式(用含n,m的式子表示,不必证明);
表达式(用含n,m的式子表示,不必证明);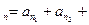 …+a
…+a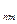 ,证明:n≤
,证明:n≤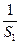 +
+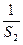 +…+
+…+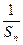 ≤
≤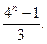
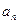 }、{
}、{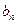 }满足:
}满足: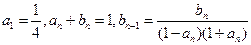 。
。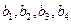 ;
;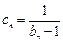 ,求数列
,求数列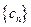 的通项公式;
的通项公式;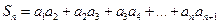 ,不等式
,不等式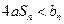 恒成立时,求实数
恒成立时,求实数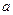 的取值范围。
的取值范围。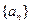 中,已知
中,已知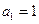 ,且
,且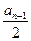 是1与
是1与
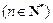 的等差中项.
的等差中项.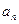 ;
;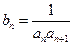 ,记数列
,记数列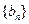 的前
的前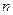 项和为
项和为 ,证明:
,证明: