题目内容
选做题:请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题记分
22.(本小题满分10分)选修4—1几何证明选讲
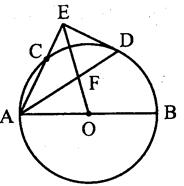
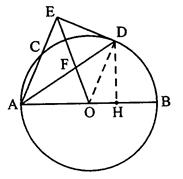
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F。
(I)求证:DE是⊙O的切线;
(II)若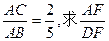 的值.
的值.
23.(本小题满分10分)选修4—2坐标系与参数方程
设直角坐标系原点与极坐标极点重合,x轴正半轴与极轴重合,若已知曲线C的极坐标方程为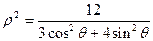 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为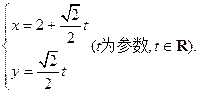
(I)求直线l的普通方程和曲线C的直角坐标方程;
(II)求曲线C上的动点P到直线l的最大距离。
24.(本小题满分10分)选修4—5不等式选讲
对于任意的实数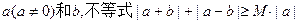 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。
(1)求m的值;
(2)解不等式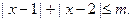
22.(本小题满分10分)选修4—1几何证明选讲
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F。
(I)求证:DE是⊙O的切线;
(II)若
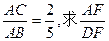 的值.
的值.
23.(本小题满分10分)选修4—2坐标系与参数方程
设直角坐标系原点与极坐标极点重合,x轴正半轴与极轴重合,若已知曲线C的极坐标方程为
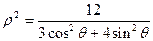 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为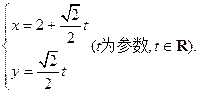
(I)求直线l的普通方程和曲线C的直角坐标方程;
(II)求曲线C上的动点P到直线l的最大距离。
24.(本小题满分10分)选修4—5不等式选讲
对于任意的实数
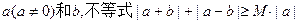 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。(1)求m的值;
(2)解不等式
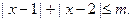
略
22.(I)证明:连结OD,可得∠ODA=∠OAD=∠DAC …………2分
∴OD//AE 又AE⊥DE …………3分
∴OE⊥OD,又OD为半径
∴DE是的⊙O切线 …………5分
(II)解:过D作DH⊥AB于H,则有∠DOH=∠CAB
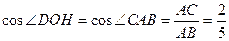 ………6分
………6分
设OD=5x,则AB=10x,OH=2x,
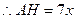 ………………7分
………………7分
由△AED≌△AHD可得AE="AH=7x " ………8分
又由△AEF∽△DOF 可得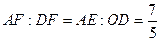
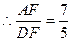 …………10分
…………10分
23.解:(I)直线l普通方程为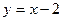 …………3分
…………3分
椭圆C的普通方程为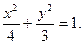 …………6分
…………6分
(II)由椭圆的普通方程可以得到其参数方程为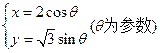
则动点 的距离为
的距离为
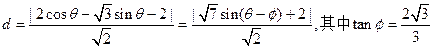 ………8分
………8分
由于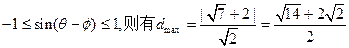 …………10分
…………10分
24.解:(I)不等式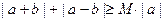 恒成立,
恒成立,
即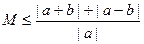 对于任意的实数
对于任意的实数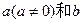 恒成立,
恒成立,
只要左边恒小于或等于右边的最小值。 …………2分
因为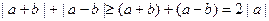 ,
,
当且仅当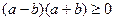 时等号成立,
时等号成立,
即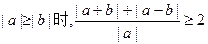 成立,
成立,
也就是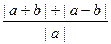 的最小值是2。…………5分
的最小值是2。…………5分
(2)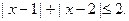 解法1:利用绝对值的意义得:
解法1:利用绝对值的意义得: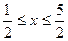
解法2:当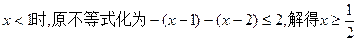 ,
,
所以x的取值范围是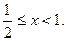
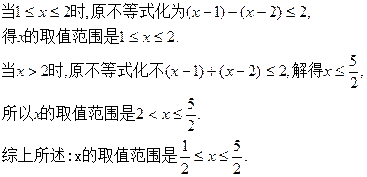
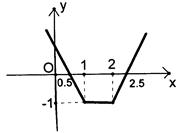
解法3:构造函数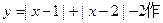
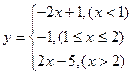 的图象,利用图象有
的图象,利用图象有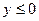 得:
得: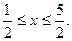 ………………10分
………………10分
∴OD//AE 又AE⊥DE …………3分
∴OE⊥OD,又OD为半径
∴DE是的⊙O切线 …………5分
|
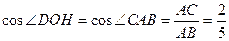 ………6分
………6分设OD=5x,则AB=10x,OH=2x,
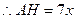 ………………7分
………………7分由△AED≌△AHD可得AE="AH=7x " ………8分
又由△AEF∽△DOF 可得
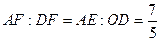
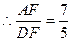 …………10分
…………10分23.解:(I)直线l普通方程为
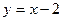 …………3分
…………3分椭圆C的普通方程为
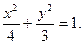 …………6分
…………6分(II)由椭圆的普通方程可以得到其参数方程为
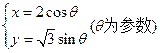
则动点
 的距离为
的距离为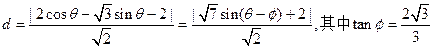 ………8分
………8分由于
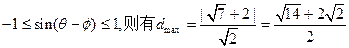 …………10分
…………10分24.解:(I)不等式
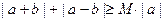 恒成立,
恒成立,即
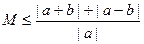 对于任意的实数
对于任意的实数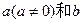 恒成立,
恒成立,只要左边恒小于或等于右边的最小值。 …………2分
因为
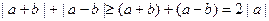 ,
,当且仅当
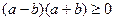 时等号成立,
时等号成立,即
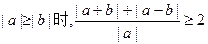 成立,
成立,也就是
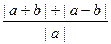 的最小值是2。…………5分
的最小值是2。…………5分(2)
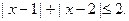 解法1:利用绝对值的意义得:
解法1:利用绝对值的意义得: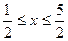
解法2:当
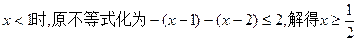 ,
,所以x的取值范围是
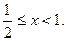
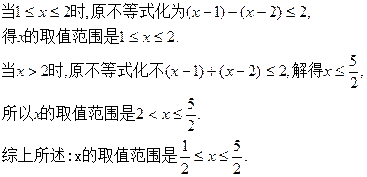
解法3:构造函数
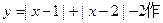
|
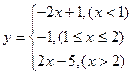 的图象,利用图象有
的图象,利用图象有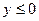 得:
得: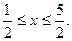 ………………10分
………………10分
练习册系列答案
相关题目
 ,
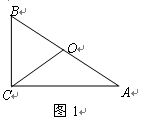
,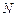 分别为锐角三角形
分别为锐角三角形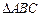 (
(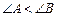 )的外接圆
)的外接圆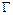 上弧
上弧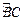 、
、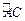 的中点.过点
的中点.过点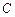 作
作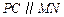 交圆
交圆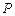 点,
点,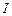 为
为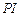 并延长交圆
并延长交圆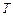 .
.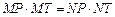 ;
;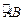 (不含点
(不含点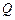 (
(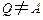 ,
,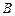 ),记
),记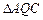 ,
,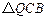 的内心分别为
的内心分别为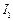 ,
,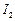 ,
,
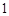 ,在
,在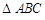 中,
中,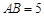 ,
,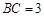 ,
,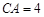 ,且
,且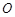 是
是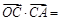
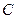 过点
过点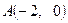 ,且与圆
,且与圆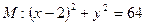 相内切.
相内切.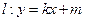 (其中
(其中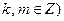 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点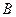 ,D,与双曲线
,D,与双曲线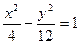 交于不同两点
交于不同两点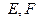 ,问是否存在直线
,问是否存在直线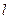 ,使得向量
,使得向量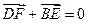 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. :
: ,
, 是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆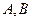 两点,求动弦
两点,求动弦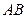 的中点
的中点 的轨迹方程
的轨迹方程 表示圆,则k的取值范围是
表示圆,则k的取值范围是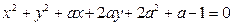 表示圆,则a的取值范围是( )
表示圆,则a的取值范围是( )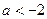
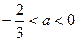
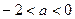
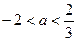
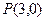 做圆
做圆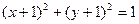 的切线,切点为点
的切线,切点为点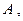 则
则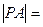 .
.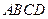 内接于
内接于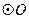 ,且
,且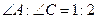 ,则
,则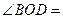 ______.
______.