题目内容
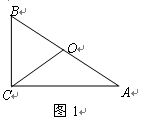
如图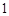 ,在
,在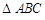 中,
中,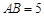 ,
,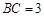 ,
,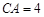 ,且
,且 是
是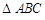 的外心,则
的外心,则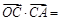
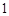 ,在
,在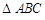 中,
中,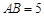 ,
,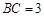 ,
,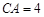 ,且
,且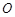 是
是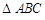 的外心,则
的外心,则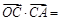
A.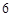 | B.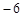 |
C.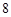 | D.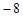 |

D
先根据三角形边的关系判断三角形的形状,结合直角三角形的性质可得到OC的长度和∠OCA的余弦值,进而可求得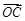 与
与 的夹角的余弦值,最后根据向量的数量积运算法可求得答案.
的夹角的余弦值,最后根据向量的数量积运算法可求得答案.
解答:解:∵在△ABC中,AB=5,BC=3,CA=4∴△ABC是直角三角形
∵O是△ABC的外心∴OC=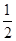 AB=
AB=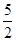 ,∠OCA=∠OAC
,∠OCA=∠OAC
∴cos∠OCA=cos∠OAC=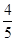
设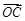 与
与 的夹角为θ,则
的夹角为θ,则
cosθ=cos(π-∠OCA)=-cos∠OCA=-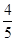
∴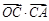 =|
=|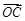 |×|
|×| |cosθ=
|cosθ=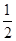 ×4×(-
×4×(-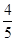 )=-8
)=-8
故选D.
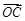 与
与 的夹角的余弦值,最后根据向量的数量积运算法可求得答案.
的夹角的余弦值,最后根据向量的数量积运算法可求得答案.解答:解:∵在△ABC中,AB=5,BC=3,CA=4∴△ABC是直角三角形
∵O是△ABC的外心∴OC=
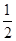 AB=
AB=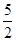 ,∠OCA=∠OAC
,∠OCA=∠OAC∴cos∠OCA=cos∠OAC=
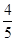
设
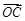 与
与 的夹角为θ,则
的夹角为θ,则cosθ=cos(π-∠OCA)=-cos∠OCA=-
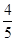
∴
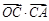 =|
=|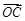 |×|
|×| |cosθ=
|cosθ=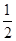 ×4×(-
×4×(-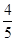 )=-8
)=-8故选D.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 的半圆上有两点
的半圆上有两点 ,设
,设 与
与 的交点是
的交点是 .
.

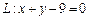 和圆
和圆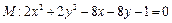 ,点
,点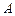 在直线
在直线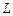 上,
上,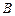 ,
,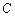 为圆
为圆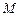 上两点,在
上两点,在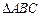 中,
中,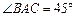 ,
,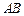 过圆心
过圆心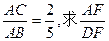 的值.
的值.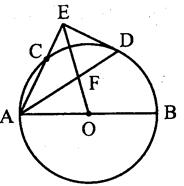
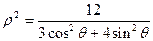 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为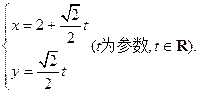
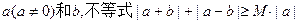 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。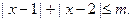
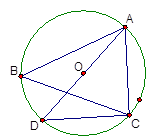
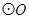 是
是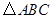 的外接圆,
的外接圆,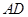 是
是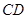 ,若
,若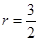 ,
,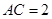 ,则
,则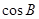 的值是( ).
的值是( ).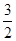
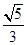
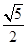

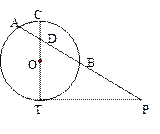
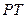 切圆
切圆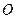 于点
于点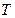 ,
,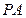 交圆
交圆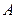 、
、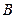 两点,且与直径
两点,且与直径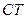 交于点
交于点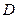 ,
,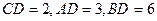 ,
, 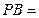 ______.
______.
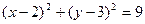 相交于A,B两点,则|AB|的最小值为( )
相交于A,B两点,则|AB|的最小值为( )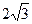
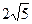
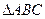 是圆的内接三角形,PA切圆于点A,PB交圆于点D。若
是圆的内接三角形,PA切圆于点A,PB交圆于点D。若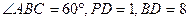 ,则
,则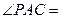 ,PA= 。
,PA= 。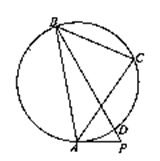
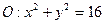 上的两点,且|AB=6,若以AB为直径的圆M恰好经过点C(1,-1),则圆心M的轨迹方程是________。
上的两点,且|AB=6,若以AB为直径的圆M恰好经过点C(1,-1),则圆心M的轨迹方程是________。