题目内容
14.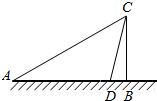 如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )| A. | 50($\sqrt{3}$+1)m | B. | 50($\sqrt{2}$+1)m | C. | 50($\sqrt{3}$-1)m | D. | 50($\sqrt{3}$+$\sqrt{2}$) m |
分析 设BC=x,在Rt△ABC中表示出AB,在Rt△CBD中表示出BD,再由AD=200m,可得出方程,解出即可.
解答 解:设BC=x,
在Rt△ABC中,AB=BCcot30°=$\sqrt{3}$x,
在Rt△CBD中,BD=CBcot75°=(2-$\sqrt{3}$)x,
则(2$\sqrt{3}-2$)x=200,
解得:x=50($\sqrt{3}$+1)m.
故选:A.
点评 本题考查了解直角三角形的应用,解答本题的关键是熟练掌握锐角三角函数的定义.

练习册系列答案
相关题目
2.执行下面的程序框图,则输出的m的值为( )
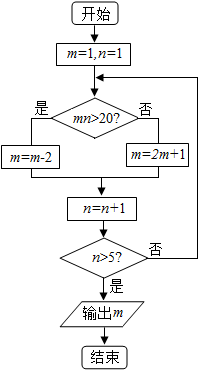

| A. | 9 | B. | 7 | C. | 5 | D. | 11 |
 如图,该程序框图的算法思路源于我国古代数学专著《九章算术》中的“更相减损术”,执行此程序框图,若输入的m,n分别为72,168,则输出的m=( )
如图,该程序框图的算法思路源于我国古代数学专著《九章算术》中的“更相减损术”,执行此程序框图,若输入的m,n分别为72,168,则输出的m=( )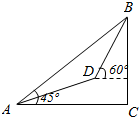 某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为$500(\sqrt{3}+1)$m.
某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为$500(\sqrt{3}+1)$m.