题目内容
【题目】已知![]() 是自然对数的底数,函数
是自然对数的底数,函数![]() 与
与![]() 的定义域都是
的定义域都是![]() .
.
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)判断函数![]() 零点个数;
零点个数;
(3)用![]() 表示
表示![]() 的最小值,设
的最小值,设![]() ,
,![]() ,若函数
,若函数![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)函数
;(2)函数![]() 只有一个零点;(3)
只有一个零点;(3)![]() .
.
【解析】
(1)先求导数![]() ,代入
,代入![]() 得
得![]() 为直线的斜率,利用点斜式可求直线方程;
为直线的斜率,利用点斜式可求直线方程;
(2)先求导数,结合导数的符号,判定零点的个数;
(3)![]() 为增函数,转化为
为增函数,转化为![]() 恒成立,然后利用分离参数法求解.
恒成立,然后利用分离参数法求解.
(1)∵![]() ,∴切线的斜率
,∴切线的斜率![]() ,
,![]() .
.
∴函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,
∴![]() 存在零点
存在零点![]() ,且
,且![]() .∵
.∵![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,由
时,由![]() 得
得
![]() .∴
.∴![]() 在
在![]() 上是减函数.
上是减函数.
∴若![]() ,
,![]() ,
,![]() ,则
,则![]() .∴函数
.∴函数![]() 只有一个零点
只有一个零点![]() ,且
,且![]() .
.
(3)解: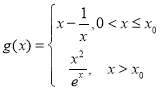 ,故
,故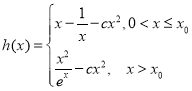 ,
,
∵函数![]() 只有一个零点
只有一个零点![]() ,∴
,∴![]() ,即
,即![]() .∴
.∴![]() .
.
∴![]() 在
在![]() 为增函数
为增函数![]() 在
在![]() ,
,![]() 恒成立.
恒成立.
当![]() 时
时![]() ,即
,即![]() 在区间
在区间![]() 上恒成立.
上恒成立.
设![]() ,只需
,只需![]() ,
,
![]() ,
,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
![]() 的最小值
的最小值![]() ,
,![]() .
.
当![]() 时,
时,![]() ,由上述得
,由上述得![]() ,则
,则![]() 在
在![]() 恒成立.
恒成立.
综上述,实数![]() 的取值范围是
的取值范围是![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.

(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年龄有关;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
(3)研究发现,某药物对新冠病毒有一定的抑制作用,需要在抽取的300人中分层选取7位60岁以下的患者做Ⅰ期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

【题目】随着社会发展对环保的要求,越来越多的燃油汽车被电动汽车取代,为了了解某品牌的电动汽车的节能情况,对某一辆电动汽车“行车数据”的两次记录如下表:
记录时间 | 累计里程 (单位:公里) | 平均耗电量(单位: | 剩余续航里程 (单位:公里) |
2020年1月1日 | 5000 | 0.125 | 380 |
2020年1月2日 | 5100 | 0.126 | 246 |
(注:累计里程指汽车从出厂开始累计行驶的路程,累计耗电量指汽车从出厂开始累计消耗的电量,![]()
![]() )
)
下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是( )
A.等于![]() B.
B.![]() 到
到![]() 之间C.等于
之间C.等于![]() D.大于
D.大于![]()