题目内容
【题目】设![]() 是等比数列的公比大于
是等比数列的公比大于![]() ,其前
,其前![]() 项和为
项和为![]() ,
,![]() 是等差数列,已知
是等差数列,已知![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的通项公式
的通项公式
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() ;
;
(3)设![]() ,其中
,其中![]() ,求
,求![]()
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设等比数列![]() 的公比为
的公比为![]() ,则
,则![]() ,设等差数列
,设等差数列![]() 的公差为
的公差为![]() ,利用等比数列的通项公式可求得
,利用等比数列的通项公式可求得![]() 的值,利用等差数列的通项公式建立有关
的值,利用等差数列的通项公式建立有关![]() 和
和![]() 的方程组,解出这两个未知数,再利用等比数列和等差数列的通项公式可求得这两个数列的通项公式;
的方程组,解出这两个未知数,再利用等比数列和等差数列的通项公式可求得这两个数列的通项公式;
(2)由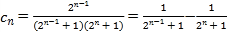 ,利用裂项相消法可求得
,利用裂项相消法可求得![]() ;
;
(3)求得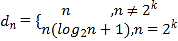 ,可得
,可得![]() ,通过分组求和以及错位相减法即可得出结果.
,通过分组求和以及错位相减法即可得出结果.
(1)设等比数列![]() 的公比为
的公比为![]() ,则
,则![]() ,设等差数列
,设等差数列![]() 的公差为
的公差为![]() ,
,
![]() ,由
,由![]() ,得
,得![]() ,
,![]() ,解得
,解得![]() ,则
,则![]() .
.
由![]() ,
,![]() 得
得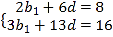 ,解得
,解得![]() ,则
,则![]() ;
;
(2)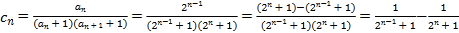 ,
,
![]() ;
;
(3)由![]() ,其中
,其中![]()
可得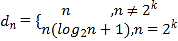 ,
,![]()
![]() ,
,
其中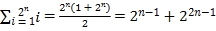 ,
,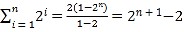
设![]() ,
,
则![]() ,
,
两式相减得![]()
整理得![]() ,
,
则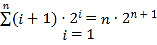 ,
,
![]() .
.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目