题目内容
若函数f(x)=sin2ax-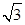 sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为
sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为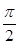 .
.
(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且x0∈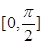 ,求点A的坐标.
,求点A的坐标.
(1)m=-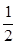 或m=
或m=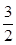 ,a=2(2)
,a=2(2) 或
或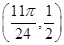 .
.
解析试题分析:(1)先通过二倍角公式、两角和与差的正弦公式将函数f(x)化简为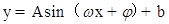 的形式,根据T=
的形式,根据T=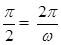 可求出a,函数f(x)的最大值等于m等于A+b可求m的值.
可求出a,函数f(x)的最大值等于m等于A+b可求m的值.
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且x0∈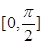 ,求出x=
,求出x=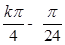 ,利用0≤
,利用0≤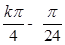 ≤
≤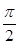 ,求出点A的坐标..
,求出点A的坐标..
试题解析:解:.(1)f(x)=sin2ax-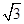 sinaxcosax
sinaxcosax
=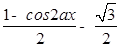 sin2ax=
sin2ax=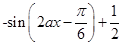 ,
,
由题意知,m为f(x)的最大值或最小值,
所以m=-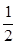 或m=
或m=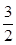 ;
;
由题设知,函数f(x)的周期为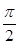 ,∴a=2,
,∴a=2,
所以m=-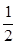 或m=
或m=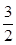 ,a=2.
,a=2.
(2)∵f(x)=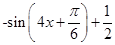 ,
,
∴令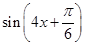 =0,得4x+
=0,得4x+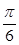 =kπ(k∈Z),
=kπ(k∈Z),
∴x=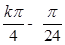 (k∈Z),
(k∈Z),
由0≤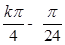 ≤
≤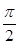 (k∈Z),得k=1或k=2,
(k∈Z),得k=1或k=2,
因此点A的坐标为 或
或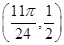 .
.
考点:1.由y=Asin(ωx+φ)的部分图象确定其解析式;2.正弦函数的对称性.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 ≤x≤9.
≤x≤9. (
(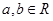 ),其图像在
),其图像在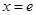 处的切线方程为
处的切线方程为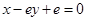 .函数
.函数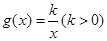 ,
, .
.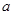 、
、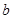 的值;
的值;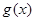 图像上一点为圆心,2为半径作圆
图像上一点为圆心,2为半径作圆 ,若圆
,若圆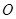 的距离为1,求
的距离为1,求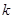 的取值范围;
的取值范围;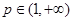 ,存在实数
,存在实数 、
、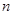 满足
满足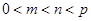 ,使得
,使得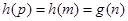 .
.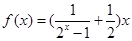 .
. 的奇偶性;(3)求证:
的奇偶性;(3)求证: 的焦点为
的焦点为 ,点
,点 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4, .
. 是抛物线上的两点,
是抛物线上的两点,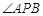 的角平分线与
的角平分线与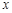 轴垂直,求
轴垂直,求 的面积最大时直线
的面积最大时直线 的方程.
的方程.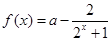 (
(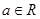 ).
). 的单调性;
的单调性;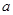 使函数
使函数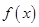 在定义域
在定义域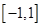 是奇函数,当
是奇函数,当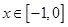 时,
时,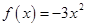 .
.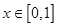 ,求
,求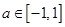 ,
,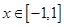 ,不等式
,不等式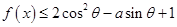 都成立,求
都成立,求 的取值范围.
的取值范围. 在[1,4]上的最值.
在[1,4]上的最值.