题目内容
对于函数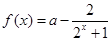 (
(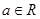 ).
).
(1)探索并证明函数 的单调性;
的单调性;
(2)是否存在实数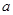 使函数
使函数 为奇函数?若有,求出实数
为奇函数?若有,求出实数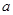 的值,并证明你的结论;若没有,说明理由.
的值,并证明你的结论;若没有,说明理由.
(1)单调增;(2)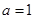 .
.
解析试题分析:(1)直接利用增函数的定义证明;(2)法一:直接用定义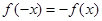 ,可得
,可得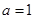 ,法二:先由
,法二:先由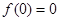 求得
求得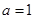 ,再证明
,再证明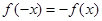 恒成立.
恒成立.
试题解析:(1)任取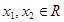 ,且
,且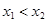 ,则
,则
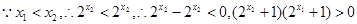 ,
,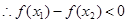 ,
,
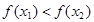 ,得
,得 在R上是增函数; (6分)
在R上是增函数; (6分)
(2)由 ,得
,得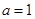 ,
,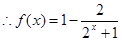 ,又
,又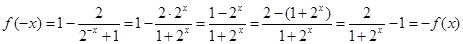
所以当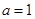 时,
时, 为奇函数. (12分)
为奇函数. (12分)
考点:(1)函数的单调性的定义;(2)函数的奇偶性.

练习册系列答案
相关题目
 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为 .
.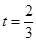 时,求直路
时,求直路
 的定义域为E,值域为F.
的定义域为E,值域为F.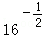 与集合F的关系;
与集合F的关系;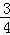 },求实数a的值.
},求实数a的值.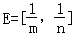 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.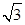 sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为
sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为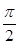 .
.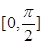 ,求点A的坐标.
,求点A的坐标.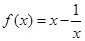 ,
,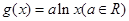 .
.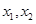 ,其中
,其中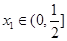 ,求
,求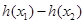 的最小值.
的最小值. 的图象分别与
的图象分别与 轴相交于两点
轴相交于两点 ,且向量
,且向量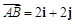 (
( 分别是与
分别是与 .
. 的值;
的值; 的解集为
的解集为 ,求
,求 的值
的值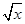 +2)=x+4
+2)=x+4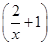 =lgx,求f(x);
=lgx,求f(x);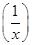 =2x,x∈R且x≠0,求f(x);
=2x,x∈R且x≠0,求f(x); 时,f
时,f >f
>f ;
; <0.
<0. (
( 为常数,且
为常数,且 ).
). 时,求函数
时,求函数 的最小值(用
的最小值(用 使得
使得 ,
, ,并且
,并且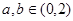 ,若存在,求出实数
,若存在,求出实数