Question

【题目】(2015·陕西）在直角坐标系xOy中，直线l的参数方程为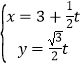（t为参数）．以原点为极点，x轴正半轴为极轴建立极坐标系，c的极坐标方程为=2sin．
（1）写出c的直角坐标方程；
（2）P为直线l上一动点，当P到圆心C的距离最小时，求P的直角坐标．

Answer 1

【答案】
（1）

x2+(y)2=3

（2）

(3,0)

【解析】（I）由=2sin, 得=2sin，
从而有. x2+y2=2y, 所以x2+(y)2=3
(II)设P（3+t, t）， 又C（0， ）,则|
故当t=0时，|PC|取最小值，此时P点的直角坐标为（3，0）.
本题主要考查的是极坐标方程化为直角坐标方程、参数的几何意义和二次函数的性质，属于容易题．解决此类问题的关键是极坐标方程或参数方程转化为平面直角坐标系方程，并把几何问题代数化．