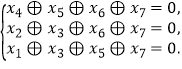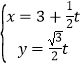题目内容
【题目】端午节吃粽子是我国的传统习俗，设一盘中装有10个粽子，其中豆沙粽2个，肉粽3个，白粽5个，这三种粽子的外观完全相同，从中任意选取3个。
（1）求三种粽子各取到1个的概率；
（2）设X表示取到的豆沙粽个数，求X的分布列与数学期望
【答案】
（1）
（2）X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
故
【解析】（1）.令
表示事件”三个粽子各取到1个“，则由古典概型的概率计算公式有
.
（2）
X的所有可能取值为0，1，2，且
综上知，X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
故
本题属于古典概型，从10个棕子中任取3个，基本事件的总数为
，其中事件“三种棕子各取1个”含基本事件的个数为
，根据古典概型概率计算公式可计算得所求概率；（2）由于10个棕子中有2个豆沙棕，因此
的可能值分另快0,1,2，同样根据古典概型概率公式可得相应的戳率，从而列出其分布列，并根据期望公式求得期望为
.
练习册系列答案
相关题目
【题目】某同学用“五点法”画函数
在某一个周期内的图象时，列表并填入了部分数据，如下表：
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 5 | -5 | 0 |
（Ⅰ）请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数
的解析式；
（Ⅱ）将
图象上所有点向左平行移动
个单位长度，得到
的图象. 若图象的一个对称中心为
，求
的最小值.
