题目内容
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面ADD1A1和侧面CDD1C1都是矩形,BC∥AD,△ABD是边长为2的正三角形,E,F分别为AD,A1D1的中点. 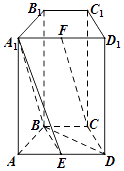
(Ⅰ)求证:DD1⊥平面ABCD;
(Ⅱ)求证:平面A1BE⊥平面ADD1A1;
(Ⅲ)若CF∥平面A1BE,求棱BC的长度.
【答案】解:(Ⅰ)证明:因为侧面ADD1A1和侧面CDD1C1都是矩形,
所以DD1⊥AD,且DD1⊥CD.
因为AD∩CD=D,
所以DD1⊥平面ABCD.
(Ⅱ)证明:因为△ABD是正三角形,且E为AD中点,
所以BE⊥AD.
因为DD1⊥平面ABCD,
而BE平面ABCD,
所以BE⊥DD1.
因为AD∩DD1=D,
所以BE⊥平面ADD1A1.
因为BE平面A1BE,
所以平面A1BE⊥平面ADD1A1.
(Ⅲ)解:因为BC∥AD,F为A1D1的中点,
所以BC∥A1F.
所以B、C、F、A1四点共面.
因为CF∥平面A1BE,
而平面BCFA1∩平面A1BE=A1B,
所以CF∥A1B.
所以四边形BCFA1是平行四边形.
所以 ![]()
【解析】(Ⅰ)证明DD1⊥AD,且DD1⊥CD,即可证明:DD1⊥平面ABCD;(Ⅱ)证明BE⊥平面ADD1A1.即可证明:平面A1BE⊥平面ADD1A1;(Ⅲ)证明四边形BCFA1是平行四边形,求棱BC的长度.
【考点精析】通过灵活运用直线与平面平行的判定和直线与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题.