题目内容
(12分)设函数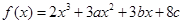 在
在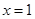 及
及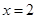 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的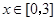 ,都有
,都有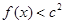 成立,求c的取值范围.
成立,求c的取值范围.
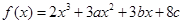 在
在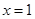 及
及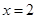 时取得极值.
时取得极值.(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的
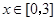 ,都有
,都有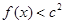 成立,求c的取值范围.
成立,求c的取值范围. (Ⅰ) ,
, .(Ⅱ)
.(Ⅱ) 。
。
 ,
, .(Ⅱ)
.(Ⅱ) 。
。本试题主要是考查了导数在研究函数中的运用。:函数在某点存在极值的性质,函数恒成立问题题,而函数①f(x)<c2在区间[a,b]上恒成立与②存在x∈[a,b],使得f(x)<c2是不同的问题.①?f(x)max<c2,②?f(x)min<c2,在解题时要准确判断是“恒成立”问题还是“存在”问题.在解题时还要体会“转化思想”及“方程与函数不等式”的思想的应用.
(1)依题意有,f'(1)=0,f'(2)=0.求解即可.
(2)若对任意的x∈[0,3],都有f(x)<c2成立?f(x)max<c2在区间[0,3]上成立,根据导数求出函数在[0,3]上的最大值,进一步求c的取值范围.
解:(Ⅰ) ,由
,由 ,
, .解得
.解得 ,
, .
.
(Ⅱ)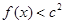 在[0,3]上恒成立即
在[0,3]上恒成立即 ,
,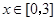
由(Ⅰ)可知, ,
, .
.
当 时,
时, ;当
;当 时,
时, ;当
;当 时,
时, .
.
即 在
在 0,1]上递增,[1,2]上递减,[2,3]上递增;∴当
0,1]上递增,[1,2]上递减,[2,3]上递增;∴当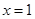 时,
时, 取得极大值
取得极大值 ,又
,又 .故当
.故当 时,
时, 的最大值为
的最大值为 .
.
于是有: ,解得
,解得  或
或 ,因此
,因此 的取值范围为
的取值范围为 。
。
(1)依题意有,f'(1)=0,f'(2)=0.求解即可.
(2)若对任意的x∈[0,3],都有f(x)<c2成立?f(x)max<c2在区间[0,3]上成立,根据导数求出函数在[0,3]上的最大值,进一步求c的取值范围.
解:(Ⅰ)
 ,由
,由 ,
, .解得
.解得 ,
, .
.(Ⅱ)
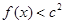 在[0,3]上恒成立即
在[0,3]上恒成立即 ,
,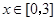
由(Ⅰ)可知,
 ,
, .
.当
 时,
时, ;当
;当 时,
时, ;当
;当 时,
时, .
.即
 在
在 0,1]上递增,[1,2]上递减,[2,3]上递增;∴当
0,1]上递增,[1,2]上递减,[2,3]上递增;∴当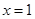 时,
时, 取得极大值
取得极大值 ,又
,又 .故当
.故当 时,
时, 的最大值为
的最大值为 .
.于是有:
 ,解得
,解得  或
或 ,因此
,因此 的取值范围为
的取值范围为 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
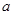 、
、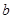 、
、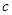 都是实数,
都是实数,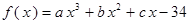 的导函数为
的导函数为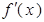 ,
,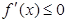 的解集为
的解集为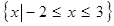 ,若
,若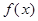 的极小值等于
的极小值等于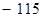 ,则
,则



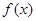 =
=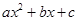 的导数为
的导数为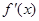 ,
,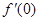 >0,对任意实数
>0,对任意实数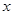 都有
都有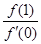 的最小值为( )
的最小值为( )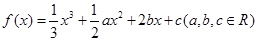 ,且函数
,且函数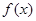 在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,则
在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,则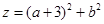 的取值范围为( )
的取值范围为( )
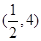


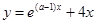 (
(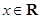 )有大于零的极值点,则实数
)有大于零的极值点,则实数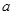 范围是 ( )
范围是 ( )



 已知
已知 在
在 时取得极值,则
时取得极值,则 等于( )
等于( )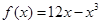 在区间
在区间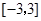 上的最小值是 .
上的最小值是 .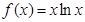 ,
,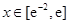 ,则
,则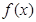 的最大值为____________,最小值为___________.
的最大值为____________,最小值为___________. ,在
,在 时有极值10,则
时有极值10,则 -
- = ▲ .
= ▲ .