题目内容
(本小题满分13分)
已知双曲线C: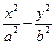 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为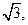 焦点到渐近线的距离为
焦点到渐近线的距离为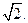
(1)求双曲线C的方程;
(2)已知直线x-y+m =0与双曲线C交于不同的两点A,B,且线段AB的中点在抛物
=0与双曲线C交于不同的两点A,B,且线段AB的中点在抛物
线y2="4" x上,求m的值.
已知双曲线C:
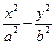 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为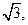 焦点到渐近线的距离为
焦点到渐近线的距离为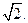
(1)求双曲线C的方程;
(2)已知直线x-y+m
 =0与双曲线C交于不同的两点A,B,且线段AB的中点在抛物
=0与双曲线C交于不同的两点A,B,且线段AB的中点在抛物线y2="4" x上,求m的值.
解:(1)由题意,得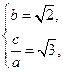 …………………3分
…………………3分
∵b2=c 2-a2=2,∴a2=1,
2-a2=2,∴a2=1,
∴所求双曲线C的方程为x2-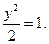 …………………6分
…………………6分
(2)设A?B两点的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),
由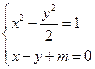 得x2-2mx-m2-2=0(判别式Δ>0),
得x2-2mx-m2-2=0(判别式Δ>0),
∴x0=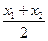 =m,y0=x0+m=2m, …………………10分
=m,y0=x0+m=2m, …………………10分
∵点M(x0,y0)在抛物线y2=4x上,
∴m=1或m=0 …………………13分
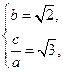 …………………3分
…………………3分∵b2=c
 2-a2=2,∴a2=1,
2-a2=2,∴a2=1,∴所求双曲线C的方程为x2-
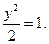 …………………6分
…………………6分 (2)设A?B两点的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),
由
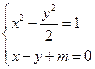 得x2-2mx-m2-2=0(判别式Δ>0),
得x2-2mx-m2-2=0(判别式Δ>0),∴x0=
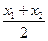 =m,y0=x0+m=2m, …………………10分
=m,y0=x0+m=2m, …………………10分∵点M(x0,y0)在抛物线y2=4x上,
∴m=1或m=0 …………………13分
略

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
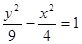 的渐近线方程是 .
的渐近线方程是 . 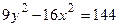 的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程。
的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程。 分)
分)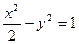 有公共渐近线,且过点
有公共渐近线,且过点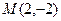 的双曲线的标准方程。
的双曲线的标准方程。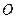 ,
,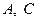 分别是双曲线虚轴的上、下顶点,
分别是双曲线虚轴的上、下顶点,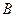 是双曲线的左顶点,
是双曲线的左顶点,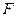 为双曲线的左焦点,直线
为双曲线的左焦点,直线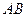 与
与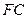 相交于点
相交于点 .若双曲线的离心率为2,则
.若双曲线的离心率为2,则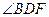 的余弦值是
的余弦值是 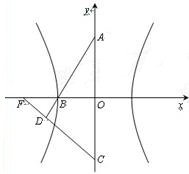
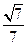
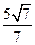
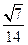
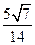
 的渐近线方程为
的渐近线方程为 ,则
,则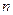 = .
= .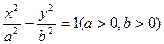 的离心率为
的离心率为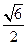 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )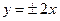



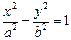
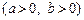 的左焦点F的直线
的左焦点F的直线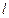 与双曲线的左支交于A、B两点,且以线段AB为直径的圆被双曲线C的左准线截得的劣弧的弧度数为
与双曲线的左支交于A、B两点,且以线段AB为直径的圆被双曲线C的左准线截得的劣弧的弧度数为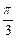 ,那么双曲线的离心率为
,那么双曲线的离心率为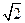
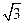
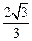
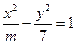 ,直线l过其左焦点
,直线l过其左焦点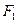 ,交双曲线左支于
,交双曲线左支于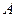 、
、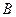 两点,且
两点,且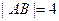 ,
,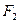 为双曲线的右焦点,
为双曲线的右焦点,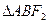 的周长为20,则m的值为
的周长为20,则m的值为