Question

【题目】已知椭圆： 的长轴长为， ， 是其长轴顶点， 是椭圆上异于， 的动点，且.

（1）求椭圆的标准方程；

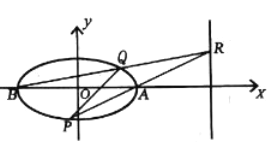
（2）如图，若动点在直线上，直线， 分别交椭圆于， 两点.请问：直线是否过定点？若是，求出定点坐标；若不是，请说明理由.

Answer 1

【答案】（1）；（2）直线过定点.

【解析】试题分析： 由长轴长为得，由，设代入计算得设直线的方程为，求出直线的方程，联立直线与椭圆方程求出， 求出直线过定点

解析：（1）由题意知则，

设， ， ，则 ，

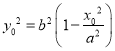由，则，则，则，由此可得椭圆的标准方程为.

（2）设，则直线的方程为；则直线的方程为联立得消去得： ，则，即代入直线的方程得，故.

联立得消去得： ，则，即代入直线的方程得，故.

当，即，则与轴交点为，

当，即时，下证直线过点，

由 ，

故直线过定点.